The KALDFS subroutine computes the smoothed state vector and its mean square error matrix from the one-step forecast and mean square error matrix computed by KALDFF.

The input arguments to the KALDFS subroutine are as follows:

data

is a matrix that contains data .

int

is an 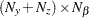vector for a time-invariant intercept, or a 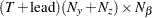vector that contains fixed matrices for the time-variant model in the transition equation and the measurement equation—that is, .

coef

is an matrix for a time-invariant coefficient, or a 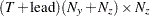matrix that contains coefficients at each time in the transition equation and the measurement equation—that is, .

var

is an 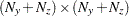matrix for a time-invariant variance matrix for transition equation noise and the measurement equation noise, or a 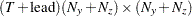matrix that contains covariance matrices for the transition equation and measurement equation errors—that is, .

bvec

is an constant vector for the intercept for the mean effect .

bmat

is an 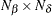matrix for the coefficient for the mean effect .

initial

is an matrix that contains an initial random vector estimate and its covariance matrix—that is, .

at

is a matrix that contains .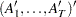

mt

is a matrix that contains .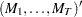

s2

is the estimated variance in the end of the data set, .

un

is an optional matrix that contains . The returned value is .

vun

is an optional 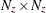matrix that contains 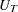. The returned value is .

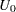The KALDFS call returns the following values:

sm

is a 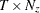matrix that contains smoothed state vectors .

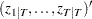vsm

is a 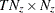matrix that contains mean square error matrices of smoothed state vectors .

Given the one-step forecast and mean square error matrix in the KALDFF call, the KALDFS call computes a smoothed state vector and its mean square error matrix. Then the KALDFS subroutine produces an estimate of the smoothed state vector at time —that is, the conditional expectation of the state vector given all observations. Using the notations and results from the KALDFF section, the backward recursion algorithm for smoothing is denoted for

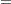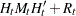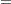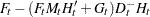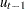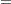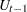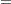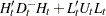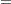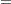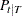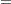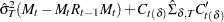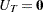where the initial values are and , and 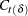is the last-column-deleted submatrix of 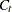. see De Jong, P. (1991) for details about smoothing in the diffuse Kalman filter.

The KALDFS call is accompanied by the KALDFF call as shown in the following statements:

ny = ncol(y);
nz = ncol(coef);
nb = ncol(int);
nd = ncol(coefd);
at = j(nz, nd+1, .);
mt = j(nz, nz, .);
qt = j(nd+1, nd+1, .);
n0 = -1;
call kaldff(pred, vpred, initial, s2, y, 0, int, coef, var, intd, 
            coefd, n0, at, mt, qt);
bvec = intd[nz+1:nz+nb,];
bmat = coefd[nz+1:nz+nb,];
call kaldfs(sm, vsm, x, int, coef, var, bvec, bmat, 
            initial, at, mt, s2);

You can also compute the smoothed estimate and its covariance matrix observation by observation. When the SSM is time invariant, the following statements perform smoothing. You should initialize UN and VUN as matrices in which all elements are zero.

n  = nrow(y);
ny = ncol(y);
nz = ncol(coef);
nb = ncol(int);
nd = ncol(coefd);
at = j(nz, nd+1, .);
mt = j(nz, nz, .);
qt = j(nd+1, nd+1, .);
n0 = -1;
call kaldff(pred, vpred, initial, s2, y, 0, int, coef, var, intd,
            coefd, n0, at, mt, qt);
bvec = intd[nz+1:nz+nb,];
bmat = coefd[nz+1:nz+nb,];
un  = j(nz, nd+1, 0);
vun = j(nz, nz, 0);
do i = 1 to n;
   call kaldfs(sm_i, vsm_i, y[n-i+1], int, coef, var, bvec, bmat, 
               initial, at, mt, s2, un, vun);
   sm  = sm_i // sm;
   vsm = vsm_i // vsm;
end;