| Language Reference |
| KALCVF Call |
The KALCVF subroutine computes the one-step prediction  and the filtered estimate
and the filtered estimate  , in addition to their covariance matrices. The call uses forward recursions, and you can also use it to obtain
, in addition to their covariance matrices. The call uses forward recursions, and you can also use it to obtain 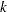 -step estimates.
-step estimates.
The input arguments to the KALCVF subroutine are as follows:
- data
is a
 matrix that contains data
matrix that contains data  .
. - lead
is the number of steps to forecast after the end of the data.
- a
is an
 vector for a time-invariant input vector in the transition equation, or a
vector for a time-invariant input vector in the transition equation, or a  vector that contains input vectors in the transition equation.
vector that contains input vectors in the transition equation. - f
is an
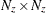 matrix for a time-invariant transition matrix in the transition equation, or a
matrix for a time-invariant transition matrix in the transition equation, or a 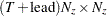 matrix that contains transition matrices in the transition equation.
matrix that contains transition matrices in the transition equation. - b
is an
 vector for a time-invariant input vector in the measurement equation, or a
vector for a time-invariant input vector in the measurement equation, or a  vector that contains input vectors in the measurement equation.
vector that contains input vectors in the measurement equation. - h
is an
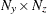 matrix for a time-invariant measurement matrix in the measurement equation, or a
matrix for a time-invariant measurement matrix in the measurement equation, or a  matrix that contains measurement matrices in the measurement equation.
matrix that contains measurement matrices in the measurement equation. - var
is an
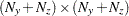 matrix for a time-invariant variance matrix for the error in the transition equation and the error in the measurement equation, or a
matrix for a time-invariant variance matrix for the error in the transition equation and the error in the measurement equation, or a  matrix that contains variance matrices for the error in the transition equation and the error in the measurement equation—that is,
matrix that contains variance matrices for the error in the transition equation and the error in the measurement equation—that is,  .
. - z0
is an optional
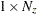 initial state vector
initial state vector  .
. - vz0
is an optional
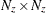 covariance matrix of an initial state vector
covariance matrix of an initial state vector  .
.
The KALCVF call returns the following values:
- pred
is a
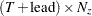 matrix that contains one-step predicted state vectors
matrix that contains one-step predicted state vectors  .
. - vpred
is a
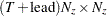 matrix that contains mean square errors of predicted state vectors
matrix that contains mean square errors of predicted state vectors 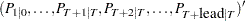 .
. - filt
is a
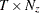 matrix that contains filtered state vectors
matrix that contains filtered state vectors  .
. - vfilt
is a
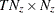 matrix that contains mean square errors of filtered state vectors
matrix that contains mean square errors of filtered state vectors  .
.
The KALCVF call computes the conditional expectation of the state vector  given the observations, assuming that the mean and the variance of the initial state vector are known. The filtered value is the conditional expectation of the state vector
given the observations, assuming that the mean and the variance of the initial state vector are known. The filtered value is the conditional expectation of the state vector  given the observations up to time
given the observations up to time  . For
. For 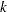 -step forecasting where
-step forecasting where  , the conditional expectation at time
, the conditional expectation at time  is computed given observations up to
is computed given observations up to  . For notation,
. For notation, 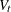 and
and  are variances of
are variances of  and
and 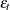 , respectively, and
, respectively, and 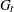 is a covariance of
is a covariance of  and
and 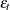 .
.  stands for the generalized inverse of
stands for the generalized inverse of 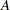 . The filtered value and its covariance matrix are denoted
. The filtered value and its covariance matrix are denoted  and
and  , respectively. For
, respectively. For  ,
, 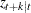 and
and  stand for the
stand for the 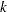 -step forecast of
-step forecast of  and its mean square error. The Kalman filtering algorithm for one-step prediction and filtering is given as follows:
and its mean square error. The Kalman filtering algorithm for one-step prediction and filtering is given as follows:
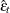 |
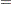 |
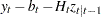 |
|||
 |
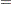 |
 |
|||
 |
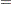 |
 |
|||
 |
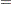 |
 |
|||
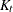 |
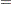 |
 |
|||
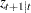 |
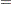 |
 |
|||
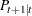 |
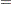 |
 |
And for 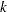 -step forecasting for
-step forecasting for  ,
,
 |
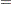 |
 |
|||
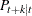 |
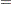 |
 |
When you use the alternative transition equation
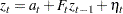 |
the forward recursion algorithm is written
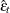 |
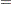 |
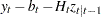 |
|||
 |
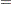 |
 |
|||
 |
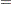 |
 |
|||
 |
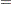 |
 |
|||
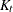 |
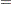 |
 |
|||
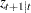 |
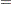 |
 |
|||
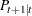 |
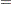 |
 |
And for 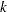 -step forecasting
-step forecasting  ,
,
 |
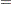 |
 |
|||
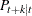 |
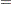 |
 |
You can use the KALCVF call when you specify the alternative transition equation and  .
.
The initial state vector and its covariance matrix of the time invariant Kalman filters are computed under the stationarity condition
 |
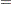 |
 |
|||
 |
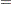 |
 |
where  and
and 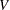 are the time-invariant transition matrix and the covariance matrix of transition equation noise, and vec
are the time-invariant transition matrix and the covariance matrix of transition equation noise, and vec is an
is an  column vector that is constructed by the stacking
column vector that is constructed by the stacking  columns of matrix
columns of matrix 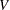 . Note that all eigenvalues of the matrix
. Note that all eigenvalues of the matrix  are inside the unit circle when the SSM is stationary. When the preceding formula cannot be applied, the initial state vector estimate
are inside the unit circle when the SSM is stationary. When the preceding formula cannot be applied, the initial state vector estimate  is set to
is set to  and its covariance matrix
and its covariance matrix  is given by
is given by  I. Optionally, you can specify initial values.
I. Optionally, you can specify initial values.
The KALCVF call accepts missing values in observations. If there is a missing observation, the filtered state vector for the missing observation is given by the one-step forecast.
The following program gives an example of the KALCVF call:
q = 2; p = 2; n = 10; lead = 3; total = n + lead; seed = 25735; x = round(10*normal(j(n, p, seed)))/10; f = round(10*normal(j(q*total, q, seed)))/10; a = round(10*normal(j(total*q, 1, seed)))/10; h = round(10*normal(j(p*total, q, seed)))/10; b = round(10*normal(j(p*total, 1, seed)))/10; do i = 1 to total; temp = round(10*normal(j(p+q, p+q, seed)))/10; var = var//(temp*temp`); end; call kalcvf(pred, vpred, filt, vfilt, x, lead, a, f, b, h, var); /* default initial state and covariance */ call kalcvs(sm, vsm, x, a, f, b, h, var, pred, vpred); print sm[format=9.4] vsm[format=9.4];
| sm | vsm | ||
|---|---|---|---|
| -1.5236 | -0.1000 | 1.5813 | -0.4779 |
| 0.3058 | -0.1131 | -0.4779 | 0.3963 |
| -0.2593 | 0.2496 | 2.4629 | 0.2426 |
| -0.5533 | 0.0332 | 0.2426 | 0.0944 |
| -0.5813 | 0.1251 | 0.2023 | -0.0228 |
| -0.3017 | 0.7480 | -0.0228 | 0.5799 |
| 1.1333 | -0.2144 | 0.8615 | -0.7653 |
| 1.5193 | -0.6237 | -0.7653 | 1.2334 |
| -0.6641 | -0.7770 | 1.0836 | 0.8706 |
| 0.5994 | 2.3333 | 0.8706 | 1.5252 |
| 0.3677 | 0.2510 | ||
| 0.2510 | 0.2051 | ||
| 0.3243 | -0.4093 | ||
| -0.4093 | 1.2287 | ||
| 0.1736 | -0.0712 | ||
| -0.0712 | 0.9048 | ||
| 1.3153 | 0.8748 | ||
| 0.8748 | 1.6575 | ||
| 8.6650 | 0.1841 | ||
| 0.1841 | 4.4770 |
Copyright © SAS Institute, Inc. All Rights Reserved.