The IFFT function computes the inverse finite Fourier transform of a matrix f, where f is an 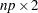numeric matrix.

The IFFT function expands a set of sine and cosine coefficients into a sequence equal to the sum of the coefficients times the sine and cosine functions. The argument f is an 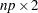matrix; the value returned is an 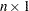vector.

If the element in the last row and second column of f is exactly 0, then is 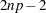; otherwise, is .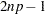

The inverse finite Fourier transform of a two column matrix 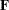, denoted by the vector , is

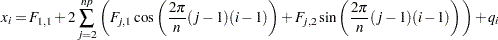for 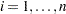, where 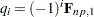if is even, or 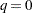if is odd.

For the most efficient use of the IFFT function, should be a power of 2. If is a power of 2, a fast Fourier transform is used (Singleton; 1969); otherwise, a Chirp-Z algorithm is used (Monro and Branch; 1976).

The expression IFFT(FFT(X)) returns times , where is the dimension of . If 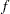is not the Fourier transform of a real sequence, then the vector generated by the IFFT function is not a true inverse Fourier transform. However, applications exist where the FFT and IFFT functions can be used for operations on multidimensional or complex data (Gentleman and Sande; 1966), (Nussbaumer; 1982).

As an example, the convolution of two vectors (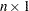) and 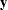(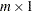) can be accomplished by using the following module:

start conv(u,v);
/* w = conv(u,v) convolves vectors u and v.
 * Algebraically, convolution is the same operation as
 * multiplying the polynomials whose coefficients are the
 * elements of u and v. Straight convolution is too slow,
 * so use the FFT.
 *
 * Both of u and v are column vectors.
 */
   m = nrow(u);
   n = nrow(v);

   wn = m + n - 1;
   /* find p so that 2##(p-1) < wn <= 2##p */
   p = ceil( log(wn)/ log(2) );
   nice = 2##p;

   a = fft( u // j(nice-m,1,0) );
   b = fft( v // j(nice-n,1,0) );
   /* complex multiplication of a and b */
   wReal = a[,1]#b[,1] - a[,2]#b[,2];
   wImag = a[,1]#b[,2] + a[,2]#b[,1];
   w = wReal || wImag;
   z=ifft(w);
   z = z[1:wn,1] / nice;  /* take real part and first wn elements */
   return (z);
finish;

/* example of convolution of two waveforms */
TimeStep = 0.01;
t = T( do(0,8,TimeStep) );

Signal = j(nrow(t),1,5);
Signal[ loc(t>4) ] = -5;

ImpulseResponse = j(nrow(t),1,0);
ImpulseResponse[ loc(t<=2) ] = 3;

/* The time domain for this convolution is [0,16]
   with the same time step.
   For waveforms, rescale amplitude by the time step. */
y = conv(Signal,ImpulseResponse) * TimeStep;

Other applications of the FFT and IFFT functions include windowed spectral estimates and the inverse autocorrelation function.