The FARMACOV subroutine computes the autocovariance function for an autoregressive fractionally integrated moving average (ARFIMA) model of the form ARFIMA().

The input arguments to the FARMACOV subroutine are as follows:

d

specifies a fractional differencing order. The value of must be in the open interval excluding zero. This input is required.

phi

specifies an 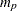-dimensional vector that contains the autoregressive coefficients, where 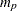is the number of the elements in the subset of the AR order. The default is zero. All the roots of should be greater than one in absolute value, where 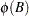is the finite-order matrix polynomial in the backshift operator 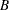, such that .

theta

specifies an 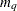-dimensional vector that contains the moving average coefficients, where 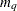is the number of the elements in the subset of the MA order. The default is zero.

p

specifies the subset of the AR order. The quantity 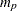is defined as the number of elements of phi.

If you do not specify p, the default subset is p.

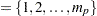For example, consider phi=0.5.

If you specify p=1 (the default), the FARMACOV subroutine computes the theoretical autocovariance function of an ARFIMA() process as

If you specify p=2, the FARMACOV subroutine computes the autocovariance function of an ARFIMA() process as

q

specifies the subset of the MA order. The quantity 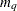is defined as the number of elements of theta.

If you do not specify q, The default subset is q.

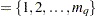The usage of q is the same as that of p.

lag

specifies the length of lags, which must be a positive number. The default is lag.

The FARMACOV subroutine returns the following value:

cov

is a lag 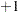vector that contains the autocovariance function of an ARFIMA() process.

As an example, consider the following ARFIMA(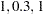) process:

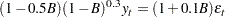In this process, . The following statements compute the autocovariance of this process:

d = 0.3;
phi = 0.5;
theta = -0.1;
sigma = 1.2;
call farmacov(cov, d, phi, theta, sigma) lag=5;
print cov;

For , the series represented as is a stationary and invertible ARFIMA(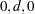) process with the autocovariance function

and the autocorrelation function

Notice that decays hyperbolically as the lag increases, rather than showing the exponential decay of the autocorrelation function of a stationary ARMA() process.

For , the series is a stationary and invertible ARFIMA() process represented as

where and and is a white noise process; all the roots of the characteristic AR and MA polynomial lie outside the unit circle.

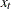Let , so that follows an ARFIMA(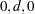) process; let , so that follows an ARMA() process; let be the autocovariance function of and be the autocovariance function of .

Then the autocovariance function of is as follows:

The explicit form of the autocovariance function of is given by Sowell (1992).