Multivariate Analysis: Correspondence Analysis

Example: Summarize the Association between Categories

In this example, you examine data from 1991 about 127 companies from five nations in four industries. The companies are from Britain, France, Germany, Japan, and the United States. The companies are in the following industries: automobiles, electronics, food, and oil.

To run a correspondence analysis:

Open the Business data set.

Table 31.1 shows a contingency table of the number of companies in each Industry for each Nation. The goal of this example is to use correspondence analysis to examine relationships between and among the Nation and Industry variables.

Table 31.1: Contingency Table of Industry and Nation

Industry	Britain	France	Germany	Japan	U.S.
	Nation
Automobiles	2	3	5	14	7
Electronics	1	3	1	12	11
Food	11	2	0	11	19
Oil	2	2	1	5	13

Select Analysis →Multivariate Analysis →Correspondence Analysis from the main menu, as shown in Figure 31.1.

Figure 31.1: Selecting the Correspondence Analysis

The Correspondence Analysis dialog box appears. (See Figure 31.2.) You can select variables for the analysis by using the Variables tab. In Table 31.1, the levels of Industry specify the rows of the table and are displayed along the vertical dimension of the table. Thus Industry is the Y variable whose values determine the rows. Similarly, Nation is the X variable whose values determine the columns.
Select Industry and click Add Y.
Select Nation and click Add X.

Figure 31.2: The Variables Tab
Click the Plots tab.

The Plots tab becomes active. (See Figure 31.3.)
Select Mosaic plot (single Y only).

Figure 31.3: The Plots Tab
Click the Tables tab.

The Tables tab becomes active. (See Figure 31.4.) For this example, it is informative to see how each cell, column, and row of Table 31.1 contributes to the chi-square association statistic for the table.
Select Contributions to chi-square statistic.

Figure 31.4: The Tables Tab
Click OK.

The analysis calls the CORRESP procedure. The procedure uses the options specified in the dialog box. The procedure displays tables in the output document, as shown in Figure 31.5. Two plots are also created.

The mosaic plot indicates the frequency count for each cell in the contingency table. You can add labels to the cells of the mosaic plot to make the frequency count more evident.
Activate the mosaic plot. Press the "l" key (lowercase "L") to toggle labels.

Figure 31.5: Output from a Correspondence Analysis

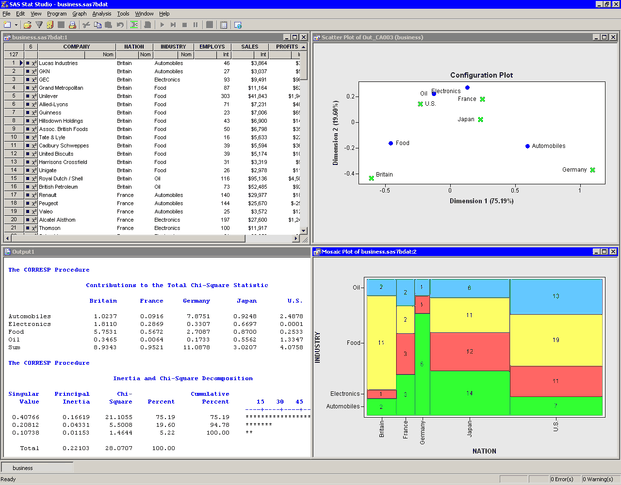
The mosaic plot shows several interesting facts. The British companies are not evenly divided among industries; many British companies in these data are food companies. Similarly, the lack of German food companies is evident, as is the preponderance of German automobile companies. The United States has the largest proportion of oil companies.

Correspondence analysis plots all the categories in a Euclidean space. The first two dimensions of this space are plotted in a configuration plot, shown in the upper right corner of Figure 31.5. As indicated by the labels for the axes, the first principal coordinate accounts for 75% of the inertia, while the second accounts for almost 20%. Thus, these two principal coordinates account for almost 95% of the inertia in this example. The plot should be thought of as two different overlaid plots, one for each categorical variable. Distances between points within a variable have meaning, but distances between points from different variables do not.

The configuration plot summarizes association between categories, and indicates the contribution to the chi-square statistic from each cell. To interpret the plot, start by interpreting the row points: the categories of Industry. The points for food and automobiles are farthest from the origin, so these industries contribute the most to the chi-square statistic. Oil and electronics contribute relatively less to the chi-square statistic.

For the column points, the points for the United States, France, and Japan are near the origin, so these countries contribute a relatively small amount to the chi-square statistic. The points for Britain and Germany are far from the origin; they make relatively large contributions to the chi-square statistic.

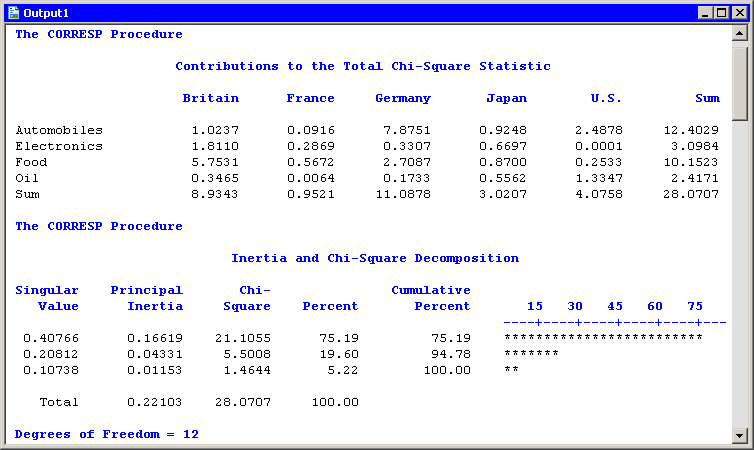
The "Contributions to the Total Chi-Square Statistic" table in Figure 31.6 displays the contributions to the chi-square statistic for each industry and country. The last column summarizes the contributions for industry. Automobiles (12.4) and food (10.15) contribute the most, a fact apparent from the configuration plot. Similarly, the last row summarizes the contributions for countries. Britain and Germany make the largest contributions.

The "Inertia and Chi-Square Decomposition" table summarizes the chi-square decomposition. The first two components account for almost 95% of the chi-square association.

Figure 31.6: Contributions to the Chi-Square Statistic

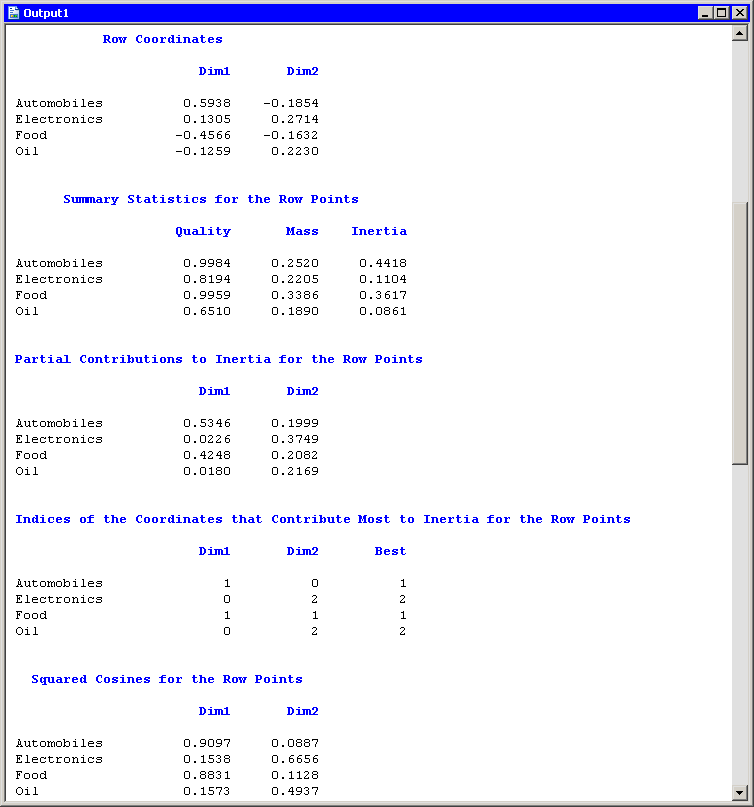
The next series of tables summarize the correspondence analysis for the row variable (Industry). These tables are shown in Figure 31.7.

The "Row Coordinates" table displays the coordinates of the various industries in the configuration plot. The "Summary Statistics" table displays various statistics, including the so-called quality of the representation. Categories with low quality values (for example, oil) are not well represented by the two principal coordinates. The quality statistic is equal to the sum of the squared cosines, which are displayed in the last table of Figure 31.7. The squared cosines are the square of the cosines of the angles between each axis and a vector from the origin to the point. Thus, points with a squared cosine near 1 are located near a principal coordinate axis, and so have high quality.

The "Partial Contributions to Inertia" table indicates how much of the total inertia is accounted for by each category in each dimension. This table corresponds to the spread of the points in the configuration plot in the horizontal and vertical dimensions. In the first principal coordinate, automobiles and food contribute the most. In the second principal coordinate, electronics contributes the most, although the contributions are more evenly spread across categories.

For further details, see the "Algorithm and Notation" and "Displayed Output" sections of the documentation for the CORRESP procedure.

Figure 31.7: Output from a Correspondence Analysis

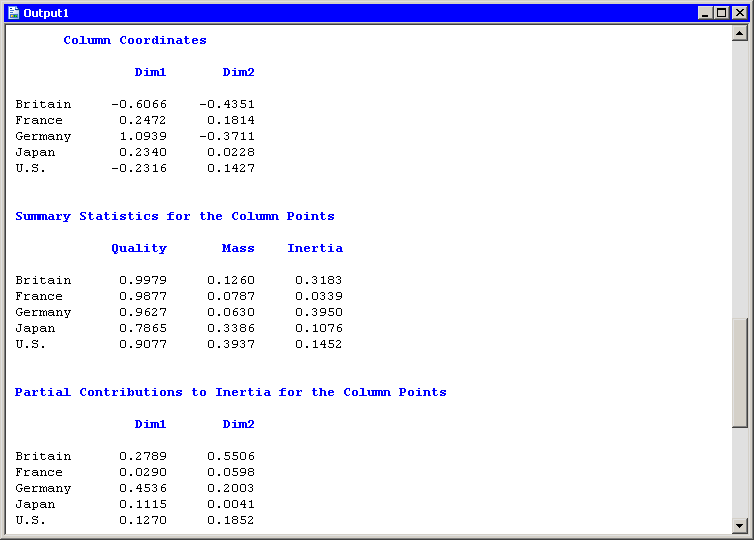
The analysis of the countries is similar. Figure 31.8 shows a partial view of the related statistics. The quality statistic helps explain a seeming discrepancy in the configuration plot. (See Figure 31.5.) From the configuration plot (and from the "Column Coordinates" table), it is apparent that the marker that represents Japan is closer to the origin than the marker that represents France. It is tempting to conclude that Japan contributes less to the chi-square statistic than France. But the "Contributions to the Total Chi-Square Statistic" table in Figure 31.6 and the "Partial Contributions to Inertia" table in Figure 31.8 show that the opposite is true.

The contradictory evidence can be resolved by noticing that the quality statistic for Japan is only 0.787. That value is the sum of the squared cosines for each dimension. The squared cosine for the second dimension is nearly zero, which indicates that Japan’s position is almost completely determined by the first dimension.

Figure 31.8: Output from a Correspondence Analysis

You cannot compare row points with column points in the configuration plot. For example, you cannot compare the distance from the origin for electronics to the distance for Japan and draw any meaningful conclusions.

However, you can interpret associations between rows and columns. For example, the first principal coordinate shows a greater association with being British and being a food company than would be expected if these two categories were independent. Similarly, the association between being German and being an automobile company is greater than expected under the assumption of independence.