Model Fitting: Generalized Linear Models
Example 2: Fit a Poisson Regression Model
In this example, you examine another example of a generalized linear model: Poisson regression. A Poisson regression analysis might be appropriate when the response variable represents counts or rates. If your explanatory variables are all nominal (that is, you can write a contingency table that contains the data), then the Poisson model is often called a log-linear model.
Counts are always nonnegative, but a linear model can predict negative values for the response. Consequently, it is common
to choose a logarithmic link function for the response. That is, if the response variable is Y and the expected value of Y is 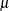 , a Poisson regression finds parameters that best fit the data to the model
, a Poisson regression finds parameters that best fit the data to the model 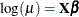 .
.
Sometimes the counts represent the number of events that occurred during an observed time period. Some counts might correspond
to longer time periods than others do. In this situation, you want to model the rate at which the events occur. When you model
a rate, you are modeling the number of events, Y, per unit of time, T. The expected value of the rate is 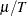 , where
, where 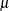 is the expected value of Y. In this case, the Poisson model is
is the expected value of Y. In this case, the Poisson model is 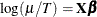 . By using the fact that
. By using the fact that 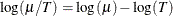 , this equation can be rewritten as
, this equation can be rewritten as
![\[ \log (\mu ) = \log (T) + \bX \bm {\beta } \]](images/imlsug_ugfitgenmod0016.png)
The term 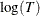 is called an offset variable.
is called an offset variable.
The example in this section fits a Poisson model to data in the Ship data set. The data and analysis are from McCullagh and Nelder (1989). The response variable, Y, is the number of damage incidents that occurred during the number of months that ship was in service (contained in the months variable). As discussed in the previous paragraph, the quantity 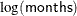 is an offset variable for this model. The three classification variables are as follows:
is an offset variable for this model. The three classification variables are as follows:
-
the ship type (
type), which contains five levels, a–e -
the year of construction (
year), which contains four levels: 1960–64, 1965–69, 1970–74, and 1975–79 -
the period of operation (
period), which contains two levels: 1960–74 and 1975–79