Distribution Analysis: Outlier Detection

Method Tab

You can use the Method tab to specify the following options for estimating the location and scale parameters for the data, and for specifying the scale multiple. The Method tab is shown in Figure 17.3.

The Method tab contains the following UI controls:

Location estimate


lists statistics that are used to estimate the location parameter for the data. Each statistic is described in the "Details" section of the UNIVARIATE procedure documentation in the Base SAS Procedures Guide. The statistics are as follows:

Mean

estimates the location parameter by using the mean of the data. ( Note: The mean is not a robust statistic; it is influenced by outliers.)

Median

estimates the location parameter by using the median of the data.

Trimmed mean

estimates the location parameter by using the trimmed mean of the data.

Winsorized mean

estimates the location parameter by using the Winsorized mean of the data.

Trimmed/Winsorized cutoff


specifies the number of observations or proportion of observations used to estimate a trimmed or Winsorized mean.

Scale estimate

lists the statistics for estimating the scale parameter for the (uncontaminated) data. The statistics are as follows:

Standard deviation

estimates the scale parameter by using the standard deviation of the data. ( Note: The standard deviation is not a robust statistic; it is influenced by outliers.)

MAD

estimates the scale parameter by using 1.4826 times the median absolute deviation from the median of the data.

Sn

estimates the scale parameter by using a specified constant times the robust statistic 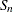$S_ n$ of the data.

Qn

estimates the scale parameter by using a specified constant times the robust statistic 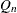$Q_ n$ of the data.

Interquartile range

estimates the scale parameter by using the interquartile range of the data divided by 1.34898.

Gini’s mean difference

estimates the scale parameter by using 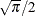$\sqrt {\pi }/2$ times Gini’s mean difference.

Scale multiplier


specifies the constant used to multiply the scale estimate. The resulting product, d, determines outliers: all values whose distance to the location estimate is greater than d are labeled as outliers.