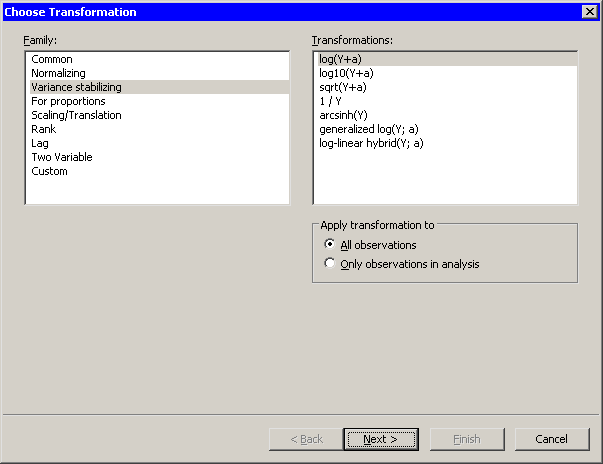
Variable Transformations
Figure 32.13 shows the transformations that are available when you select from the list. Variance stabilizing transformations are often used to transform a variable whose variance depends on the value of the variable. For example, the variability of a variable Y might increase as Y increases. Equations for these transformations are given in Table 32.3.
Table 32.3: Description of Variance Stabilizing Transformations
|
Default |
Name of |
||
|---|---|---|---|
|
Transformation |
Parameter |
New Variable |
Equation |
|
log(Y+a) |
|
Log_Y |
|
|
log10(Y+a) |
|
Log10_Y |
|
|
sqrt(Y+a) |
|
Sqrt_Y |
|
|
1 / Y |
Inv_Y |
|
|
|
arcsinh(Y) |
Arcsinh_Y |
|
|
|
generalized log(Y;a) |
|
GLog_Y |
|
|
log-linear hybrid(Y;a) |
|
LogLin_Y |
See text. |
The log-linear hybrid transformation is defined for ![]() as follows:
as follows:
The function is linear for ![]() , logarithmic for
, logarithmic for ![]() , and continuously differentiable.
, and continuously differentiable.
The generalized log and the log-linear hybrid transformations were introduced in the context of gene-expression microarray data by Rocke and Durbin (2003).