Variable Transformations

Example: Apply a Logarithmic Transformation

Many statistical analyses assume that the data are normally distributed. If a variable is not normally distributed, it is often possible to improve normality by using an appropriate transformation of the variable. The three transformations used most often for this purpose are the logarithmic, square root, and inverse transformations.

The following steps apply a logarithmic transformation to the driltime variable of the Miningx data set. Because the driltime variable is nonnegative, a logarithmic transformation is well-defined.

  1. Open the Miningx data set.

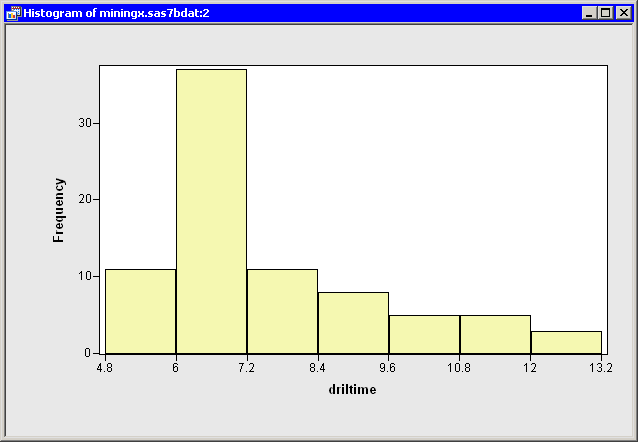
  2. Create a histogram of the driltime variable.

    The histogram is shown in Figure 32.1.

    Figure 32.1: Histogram of Drilling Time

    Histogram of Drilling Time


    Clearly, the driltime variable is not normally distributed. You might explore whether some transformation of driltime is approximately normal. To begin, you might try a logarithmic transformation.

  3. Select Analysis →Variable Transformation from the main menu.

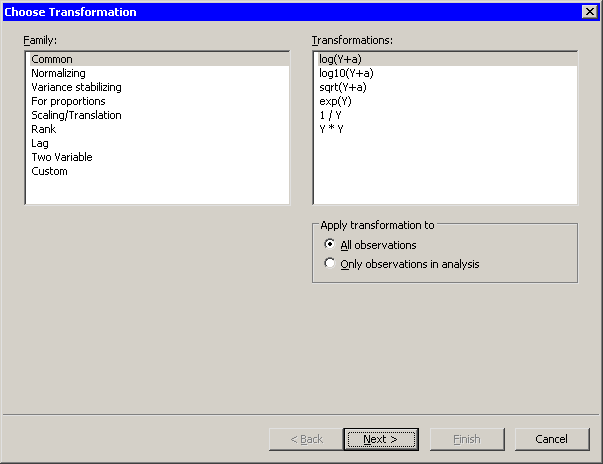
    The Variable Transformation Wizard in Figure 32.2 appears.

    Figure 32.2: Selecting a Transformation

    Selecting a Transformation


    The first page of the wizard enables you to select a transformation family and a specific transformation within that family. The logarithmic transformation is available from several items in the Family list, including the Common family. This transformation is of the form 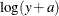$\log (y+a)$, so you need to specify the variable y and the parameter a.

    The transformation log(Y+a) is highlighted by default. Since this is the desired transformation, you can proceed to the next page of the wizard.

  4. Click Next.

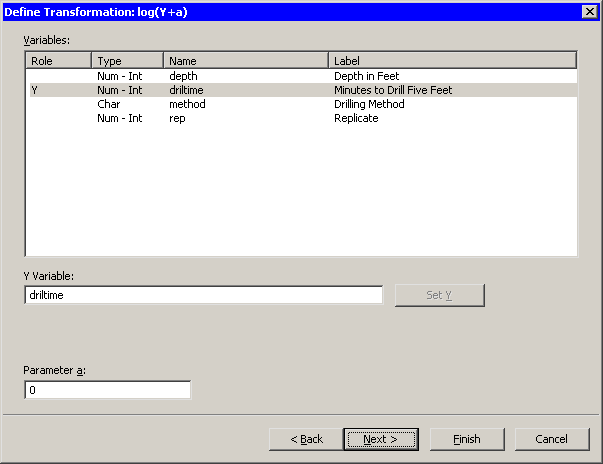
    The wizard displays the page shown in Figure 32.3. Note that the transformation appears on the page’s title bar.

    Figure 32.3: Selecting a Variable and a Parameter

    Selecting a Variable and a Parameter


  5. Select the driltime variable, and click Set Y.

    The parameter a is an offset that is useful if your variable contains nonpositive values. For these data, you can accept the default value of 0.

  6. Click Next.

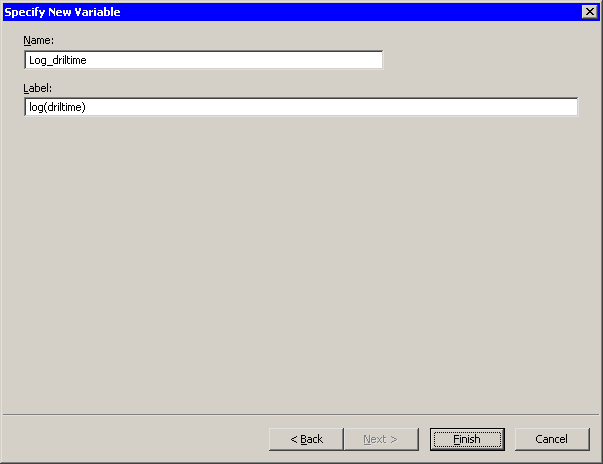
    The wizard displays the page shown in Figure 32.4. You can use this page to specify a variable name (and, optionally, a label) for the new variable.

    Figure 32.4: Specifying the Variable Name and Label

    Specifying the Variable Name and Label


    For this example, you can accept the default variable name.

  7. Click Finish.

    SAS/IML Studio adds the new variable, Log_driltime, as the last variable in the data set. You can horizontally scroll through the data table to see the variable.

    To complete this example, you can visualize the distribution of the new variable.

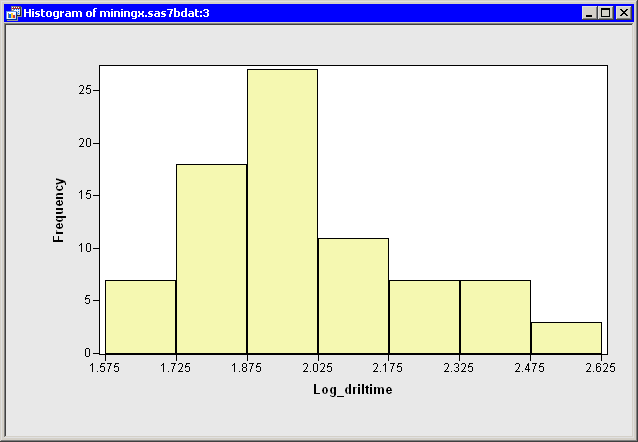
  8. Create a histogram of the Log_driltime variable.

    The histogram shows improved normality, but the transformed data distribution is still skewed to the right. (See Figure 32.5.)

Figure 32.5: A Histogram of the Transformed Data

A Histogram of the Transformed Data