Multivariate Analysis: Correlation Analysis
In this example, you explore correlations and bivariate relationships between variables in the Hurricanes data set. The data are for North Atlantic tropical cyclones from 1988 to 2003. The data set includes information about each
storm’s latitude (in the latitude variable), its sustained low-level winds (wind_kts), its central atmospheric pressure (min_pressure), and the size of its eye (radius_eye). A full description of the Hurricanes data set is included in Appendix A: Sample Data Sets.
To run a correlation analysis:
-
Select → → from the main menu, as shown in Figure 25.1.
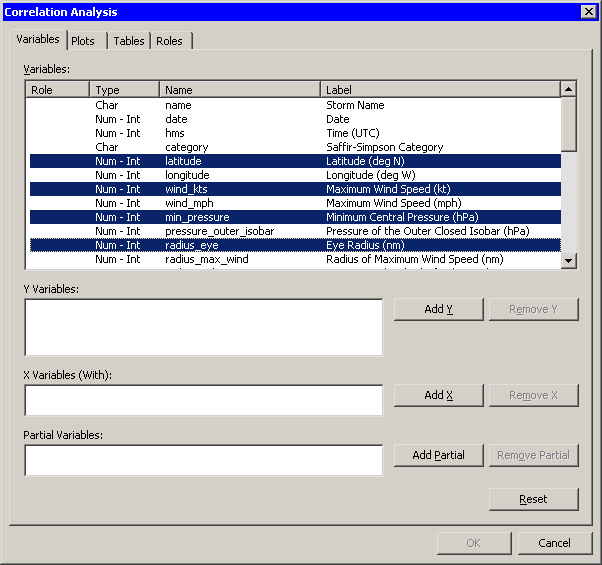
The Correlation Analysis dialog box appears. (See Figure 25.2.) You can select variables for the analysis by using the Variables tab.
-
Select
latitude. While holding down the CTRL key, selectwind_kts,min_pressure, andradius_eye, and click . -
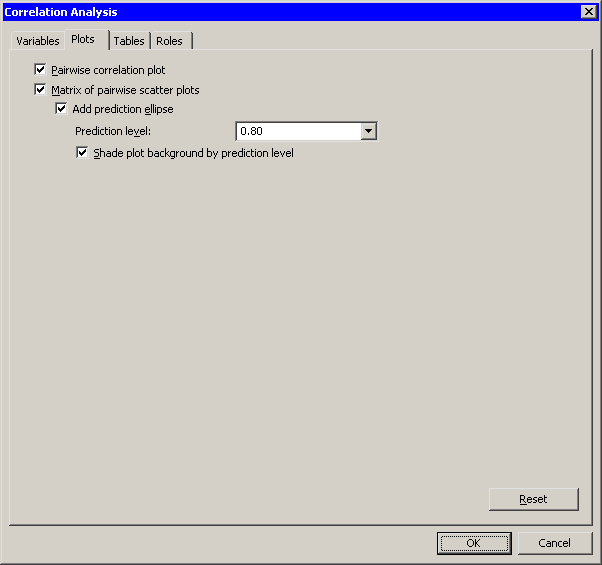
Click the Plots tab.
The Plots tab becomes active. (See Figure 25.3.)
-
Select .
-
Click .
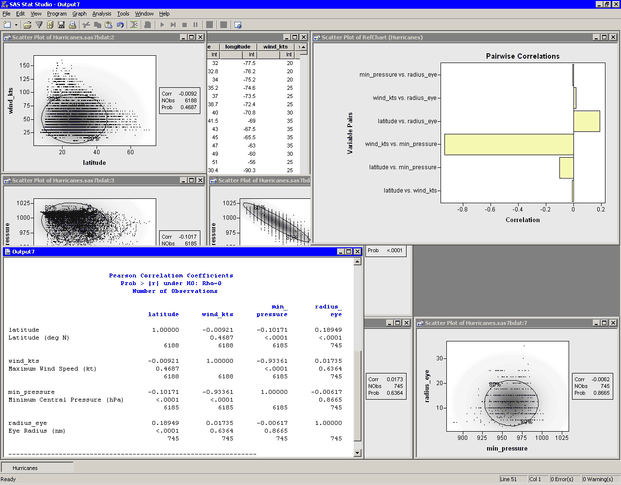
The analysis calls the CORR procedure, which uses the options specified in the dialog box. The procedure displays tables in the output document, as shown in Figure 25.4.
The "Simple Statistics" table (not shown in the figure) displays basic statistics such as the mean, standard deviation, and range of each variable.
The "Pearson Correlation Coefficients" table displays the correlation coefficients between pairs of variables. In addition, the table gives the number of nonmissing observations for each pair of variables, and tests the hypothesis that the coefficient is zero.
Note that the number of observations used to compute the correlation coefficients can vary. For example, there are no missing
values in the latitude of wind_kts variables, so the correlation coefficient for this pair is computed using all 6,188 observations in the data set. In contrast,
only 745 values for radius_eye are nonmissing, reflecting the fact that not all cyclones have well-defined eyes.
For these data, the correlation between min_pressure and wind_kts is strong and negative, with a value near 
. This is not surprising, since winds are determined by a pressure gradient. Although not as strong, there is also negative
correlation between latitude and min_pressure. In contrast, the correlation between latitude and radius_eye is positive. The correlation between the following pairs of variables is not significantly different from zero: latitude and wind_kts, radius_eye and wind_kts, and radius_eye and min_pressure.
These results are graphically summarized in the pairwise correlations plot, shown in the upper right corner of Figure 25.4. This plot is not linked to the original data set because it has a different number of observations. However, you can view the data for this plot by pressing the F9 key when the plot is active.
