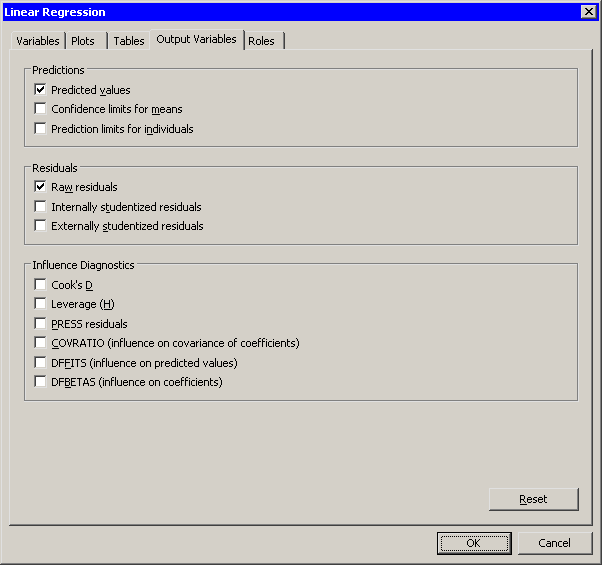
Model Fitting: Linear Regression
You can use the Output Variables tab to add analysis variables to the data table. (See Figure 21.17.) If you request a plot that uses one of the output variables, then that variable is automatically created even if you did not explicitly select the variable on the Output Variables tab.
The following list describes each output variable and indicates how the output variable is named. Y represents the name of the response variable.
- Predicted values
-
adds predicted values. The variable is namedRegP_Y. - Confidence limits for means
-
adds 95% confidence limits for the expected value (mean). The variables are namedRegLclm_Y andRegUclm_Y. - Prediction limits for individuals
-
adds 95% confidence limits for an individual prediction. The variables are namedRegLcli_Y andRegUcli_Y. - Raw residuals
-
adds residuals, which are calculated as observed values minus predicted values. The variable is namedRegR_Y. - Internally studentized residuals
-
adds internally studentized residuals, which are the residuals divided by their standard errors. (These correspond to the STUDENT= option in the OUTPUT statement.) The variable is namedRegIntR_Y. - Externally studentized residuals
-
adds externally studentized residuals, which are studentized residuals with the current observation deleted. (These correspond to the RSTUDENT= option in the OUTPUT statement.) The variable is namedRegExtR_Y. - Cook’s D
-
adds Cook’s D influence statistic. The variable is namedRegCooksD_Y. - Leverage (H)
-
adds the leverage statistic. The variable is namedRegH_Y. - PRESS residuals
-
adds the PRESS residuals. This is the ith residual divided by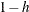 , where h is the leverage and where the model has been refit without the ith observation. The variable is named
, where h is the leverage and where the model has been refit without the ith observation. The variable is named RegPRESS_Y. - COVRATIO (influence on covariance of coefficients)
-
adds the covariance ratio. This is the ith residual divided by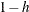 , where h is the leverage and where the model has been refit without the ith observation. The variable is named
, where h is the leverage and where the model has been refit without the ith observation. The variable is named RegCovRatio_Y. - DFFITS (influence on predicted values)
-
adds the standard influence of observation on the predicted value. The variable is namedRegDFFITS_Y. - DFBETAS (influence on coefficients)
-
adds p variables, where p is the number of parameters in the model. The variables are scaled measures of the change in each parameter estimate and are calculated by deleting the ith observation. Large values of DFBETAS indicate observations that are influential in estimating a given parameter. Belsley, Kuh, and Welsch (1980) recommend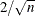 as a size-adjusted cutoff. The variables are named
as a size-adjusted cutoff. The variables are named DFB_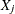 , where
, where 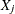 is the name of the jth regressor (including the intercept).
is the name of the jth regressor (including the intercept).