Part 3: Model the Response Variable :: SAS/IML(R) Studio 13.1: User's Guide

Part 3: Model the Response Variable

To model Log10_salary as a function of three explanatory variables:

Select Analysis →Model Fitting →Linear Regression from the main menu, as shown in Figure 21.5.

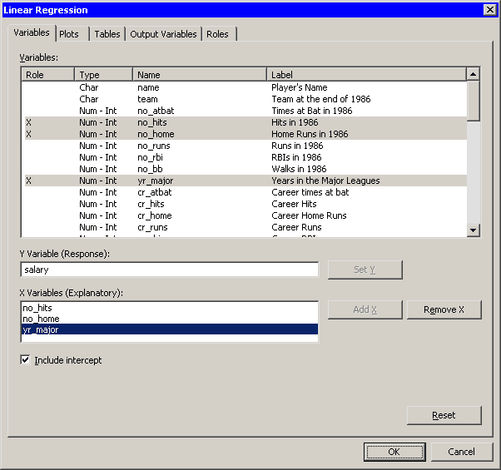
Figure 21.5: Selecting a Linear Regression

The Linear Regression dialog box appears. (See Figure 21.6.)
Scroll to the end of the variable list. Select Log10_salary, and click Set Y.
Select no_hits. While holding down the CTRL key, select no_home, and yr_major. Click Add X.

Figure 21.6: The Variables Tab
Click the Plots tab.

The Plots tab becomes active, as shown in Figure 21.7. This tab controls which graphs are produced by the analysis.
Select Cook’s D vs. Observation number.

Figure 21.7: The Plots Tab
Click the Tables tab.

The Tables tab becomes active, as shown in Figure 21.8.
Click Confidence limits for parameters.

Figure 21.8: The Tables Tab
Click OK.

Several plots appear, along with output from the REG procedure. Some plots might be hidden beneath others. Move the windows so that they are arranged as in Figure 21.9.

The Residuals vs. Predicted plot does not show any obvious trends in the residuals, although possibly the residuals are slightly higher for predicted values near the middle of the predicted range. The Observed vs. Predicted plot shows a reasonable fit, with a few exceptions.

In the output window you can see that R square is 0.5646, which means that the model accounts for 56% of the variation in the data. The no_home term is not significant ( $t=1.38$ , $p=0.1677$ ) and thus can be removed from the model. This is also seen by noting that the 95% confidence limits for the coefficient of no_home include zero.

The Cook’s $D$ plot shows how deleting any one observation would change the parameter estimates. (Cook’s $D$ and other influence statistics are described in the “Influence Diagnostics” section of the documentation for the REG procedure.) A few influential observations have been selected in the plot of Cook’s $D$ ; these observations are seen highlighted in the other plots. Three players (Steve Sax, Graig Nettles, and Steve Balboni) with high Cook’s $D$ values also have large negative residuals which indicates that they were paid less than the model predicts.

Two other players (Darryl Strawberry and Pete Rose) are also highlighted. These players are discussed in the next section.

Figure 21.9: Results from the Linear Regression Analysis