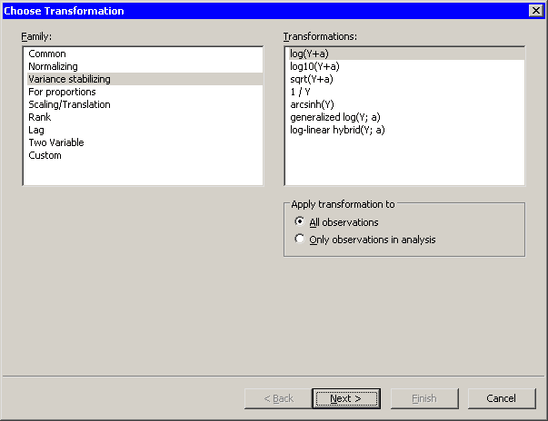
Variance Stabilizing Transformations :: SAS/IML(R) Studio 12.3: User's Guide

Variance Stabilizing Transformations

Figure 32.13 shows the transformations that are available when you select Variance stabilizing from the Family list. Variance stabilizing transformations are often used to transform a variable whose variance depends on the value of the variable. For example, the variability of a variable might increase as increases. Equations for these transformations are given in Table 32.3.

Figure 32.13: Variance Stabilizing Transformations

Table 32.3: Description of Variance Stabilizing Transformations

Transformation	Parameter	New Variable	Equation
	Default	Name of
log(Y+a)		Log_Y	$\log (Y+a), \quad Y+a>0$
log10(Y+a)		Log10_Y	$\log _{10}(Y+a), \quad Y+a>0$
sqrt(Y+a)		Sqrt_Y	$\sqrt {Y+a}, \quad Y+a>0$
1 / Y		Inv_Y	$1/Y, \quad Y\neq 0$
arcsinh(Y)		Arcsinh_Y	$\log (Y+\sqrt {Y^2+1})$
generalized log(Y;a)		GLog_Y	$\log ((Y+\sqrt {Y^2+a^2})/2)$
log-linear hybrid(Y;a)		LogLin_Y	See text.

The log-linear hybrid transformation is defined for as follows:

$H(y;a) = \left\{ \begin{array}{l l} y/a + \log (a)-1 & \mbox{if } y<a \\ \log y & \mbox{if } y \geq a \end{array} \right.$

The function is linear for , logarithmic for , and continuously differentiable.

The generalized log and the log-linear hybrid transformations were introduced in the context of gene-expression microarray data by Rocke and Durbin (2003).