Overview of Factor Analysis :: SAS/IML(R) Studio 12.3: User's Guide

Overview of Factor Analysis

Like principal component analysis, common factor analysis is a technique for reducing the complexity of high-dimensional data. (For brevity, this chapter refers to common factor analysis as simply “factor analysis.”) However, the techniques differ in how they construct a subspace of reduced dimensionality. Jackson (1981, 1991) provides an excellent comparison of the two methods.

Principal component analysis chooses a coordinate system for the vector space spanned by the variables. (Recall that the span of a set of vectors is the vector space consisting of all linear combinations of the vectors.) The first principal component points in the direction of maximum variation in the data. Subsequent components account for as much of the remaining variation as possible while being orthogonal to all of the previous principal components. Each principal component is a linear combination of the original variables. Dimensional reduction is achieved by ignoring dimensions that do not explain much variation.

While principal component analysis explains variability, factor analysis explains correlation. Suppose two variables, $\bm {x_1}$ and $\bm {x_2}$ , are correlated, but not collinear. Factor analysis assumes the existence of an unobserved variable (often called a latent variable) that is linearly related to $\bm {x_1}$ and $\bm {x_2}$ , and explains the correlation between them. The goal of factor analysis is to estimate this latent variable from the structure of the original variables. An estimate of the unobserved variable is called a common factor.

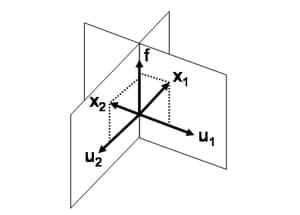
The geometry of the relationship between the original variables and the common factor is illustrated in Figure 27.1. (The figure is based on a similar figure in Wickens (1995), as is the following description of the geometry.) The correlated variables $\bm {x_1}$ and $\bm {x_2}$ are shown schematically in the figure. Each vector is decomposed into a linear combination of a common factor and a unique factor. That is, $\bm {x_ i} = c_ i \bm {f} + d_ i \bm {u_ i}$ , . The unique factors, $\bm {u_1}$ and $\bm {u_2}$ , are uncorrelated with the common factor, $\bm {f}$ , and with each other. Note that $\bm {f}$ , $\bm {u_1}$ , and $\bm {u_2}$ are mutually orthogonal in the figure.

Figure 27.1: The Geometry of Factor Analysis

In contrast to principal components, a factor is not, in general, a linear combination of the original variables. Furthermore, a principal component analysis depends only on the data, whereas a factor analysis requires fitting the theoretical structure in the previous paragraph to the observed data.

If there are variables and you postulate the existence of common factors, then each variable is represented as a linear combination of the common factors and a single unique factor. Since the unique factors are uncorrelated with the common factors and with each other, factor analysis requires dimensions. (Figure 27.1 illustrates the case and .) However, the orthogonality of the unique factors means that the geometry is readily understood by projecting the original variables onto the span of the factors (called the factor space). A graph of this projection is called a pattern plot. In Figure 27.1, the pattern plot is the two points on $\bm {f}$ obtained by projecting $\bm {x_1}$ and $\bm {x_2}$ onto $\bm {f}$ .

The length of the projection of an original variable $\bm {x}$ onto the factor space indicates the proportion of the variability of $\bm {x}$ that is shared with the other variables. This proportion is called the communality. Consequently, the variance of each original variable is the sum of the common variance (represented by the communality) and the variance of the unique factor for that variable. In a pattern plot, the communality is the squared distance from the origin to a point.

In factor analysis, the common factors are not unique. Typically an initial orthonormal set of common factors is computed, but then these factors are rotated so that the factors are more easily interpreted in terms of the original variables. An orthogonal rotation preserves the orthonormality of the factors; an oblique transformation introduces correlations among one or more factors.

You can run the Factor analysis in SAS/IML Studio by selecting Analysis →Multivariate Analysis →Factor Analysis from the main menu. The analysis is implemented by calling the FACTOR procedure in SAS/STAT software. See the FACTOR procedure documentation in the SAS/STAT User's Guide for additional details.

The FACTOR procedure provides several methods of estimating the common factors and the communalities. Since an -dimensional model is fit by using the original variables, you should interpret the results with caution. The following list describes special issues that can occur:

Some of the eigenvalues of the reduced correlation matrix might be negative. A reduced correlation matrix is the correlation matrix of the original variables, except that the 1’s on the diagonal are replaced by prior communality estimates. These estimates are less than 1, and so the reduced correlation matrix might not be positive definite. In this case, the factors that correspond to the largest eigenvalues might account for more than 100% of the common variance.
The communalities are the proportions of the variance of the original variables that can be attributed to the common factors. As such, the communalities should be in the interval . However, factor analyses that use iterative fitting estimate the communality at each iteration. For some data, the estimate might equal (or exceed) 1 before the analysis has converged to a solution. This is known as a Heywood (or an ultra-Heywood) case, and it implies that one or more unique factor has a nonpositive variance. When this occurs, the factor analysis stops iterating and reports an error.

These and other issues are described in the section “Heywood Cases and Other Anomalies about Communality Estimates” in the documentation for the FACTOR procedure.

You can use many different methods to perform a factor analysis. Two popular methods are the principal factor method and the maximum likelihood method. The principal factor method is computationally efficient and has similarities to principal component analysis. The maximum likelihood (ML) method is an iterative method that is computationally more demanding and is prone to Heywood cases, nonconvergence, and multiple optimal solutions. However, the ML method also provides statistics such as standard errors and confidence limits that help you to assess how well the model fits the data, and to interpret factors. Consequently, the ML method is often favored by statisticians.

In addition to these various methods of factor analysis, you can use SAS/IML Studio to compute various component analyses: principal component analysis, Harris component analysis, and image component analysis.