Overview of the Generalized Linear Models Analysis

The generalized linear model is a generalization of the traditional linear model. It differs from a linear model in that it assumes that the response distribution is related to the linear predictor through a function called the link function.

Specifically, a generalized linear model has a linear component

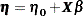and a monotonic differentiable function, 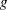, that links the expected response mean, 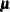, to the linear predictor :

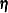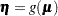The response 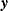is assumed to have a distribution from the exponential family (for example, normal, gamma, Poisson, binomial, and so on). The vector 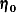is called an offset variable. As in least squares regression, 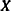is the design matrix and 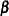is a vector of unknown parameters.

The explanatory variables in the Generalized Linear Models analysis can be interval variables or nominal variables (also known as classification variables). You can also specify more complex model terms such as interactions and nested effects.

As mentioned in Chapter 21, Model Fitting: Linear Regression, the Linear Regression analysis in SAS/IML Studio does not support classification variables. You can use the Generalized Linear Models analysis to fit a linear regression with classification variables by specifying that the response variable is normally distributed and that the link function is the identity function. The first example in this chapter demonstrates this technique. The second example in this chapter fits a Poisson regression model. The link function for this example is the 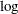function.

You can run a Generalized Linear Models analysis by selecting Analysis Model Fitting Generalized Linear Models from the main menu. The computation of the regression function and related statistics is implemented by calling the GENMOD procedure in SAS/STAT software. See the documentation for the GENMOD procedure in the SAS/STAT 9.3 User's Guide for additional details.