Adding Curves to Graphs
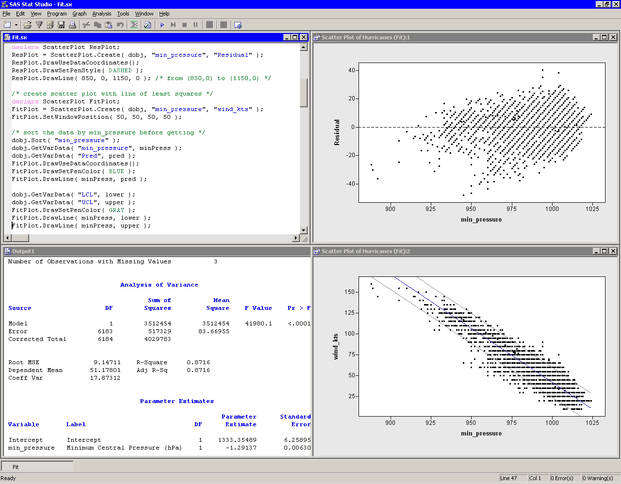
Now you will create a scatter plot of wind_kts versus min_pressure. On this plot you add the predicted values and the upper and lower confidence limits as computed by the REG procedure. This
fitted model is a straight line, which can be visualized by specifying two points as you did for the residual plot. However,
visualizing a more general parametric model (for example, a quadratic model in min_pressure) or a nonparametric model requires that you plot a polyline, so this example adopts the general approach.
A polyline is a sequence of connected line segments specified by passing two vectors to the DrawLine method. The first vector
specifies the X coordinates, and the second specifies the Y coordinates. The polyline is drawn from ![]() to
to ![]() to
to ![]() and so on until
and so on until ![]() .
.
To draw the polyline, you need a SAS/IML matrix that contains the coordinates to be plotted. You can use the GetVarData method
of the DataObject class to get the data from the DataObject. You also need to sort the data according to the X variable, which is min_pressure for this example. (Alternatively, you can use the SAS/IML SORT call if you do not want to change the order of observations
in the DataObject.)
Add the following statements at the bottom of the program window, and select → from the main menu.
declare ScatterPlot FitPlot;
FitPlot = ScatterPlot.Create( dobj, "min_pressure", "wind_kts" );
FitPlot.SetWindowPosition( 50, 50, 50, 50 );
dobj.Sort( "min_pressure" );
dobj.GetVarData( "min_pressure", minPress );
dobj.GetVarData( "Pred", pred );
FitPlot.DrawUseDataCoordinates();
FitPlot.DrawSetPenColor( BLUE );
FitPlot.DrawLine( minPress, pred );
dobj.GetVarData( "LCL", lower );
dobj.GetVarData( "UCL", upper );
FitPlot.DrawSetPenColor( GRAY );
FitPlot.DrawLine( minPress, lower );
FitPlot.DrawLine( minPress, upper );
The predicted line is drawn in blue, as specified by the DrawSetPenColor method of the Plot class. The lower and upper limits of prediction are drawn in gray. All lines are drawn on top of the observations and are drawn as solid lines with a width of one pixel, since those default values were not changed. Figure 6.2 shows the resulting plot.
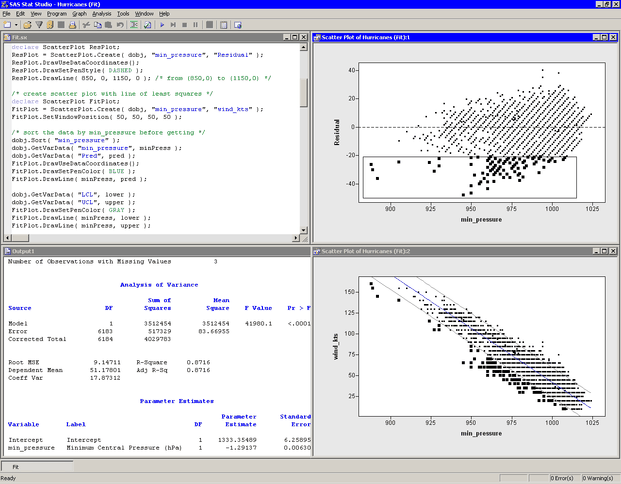
Notice that the preceding statements read variables from an output data set into a DataObject. This is possible only if the output data set has the same number of observations as the DataObject. The advantages of reading variables into the DataObject are that you can open a data table to see the values of the added variables and that you can use these variables in subsequent analyses. Furthermore, you can use the dynamically linked graphs to identify observations in a plot that have certain characteristics. For example, Figure 6.3 shows the observations that have large negative residuals for this model.
Note: Alternatively, you could have used the USE and READ statements to read the predicted values and the upper and lower limits of prediction into SAS/IML matrices. This approach is described in the next section.