The model specified using the MARKER, MODEL, RANDOM, and REPEATED statements is estimated using mixed model theory, and the resulting model statistics are printed in the "Model Statistics" table. For more details about these calculations, see the "Mixed Models Theory" section in "The MIXED Procedure" chapter in the SAS/STAT User's Guide.

If the PARMEST statement is used, a BTL model will be fit to the input data. This section describes the formulation of the BTL model and the procedure for estimating model parameters for the given data set. The section has been adapted from Coffman et al. (2005).

PROC BTL fits the input data to a probability model for multiple binary trait loci (Simonsen 2004). The assumed genetic map contains alternating markers (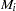) and binary trait loci (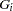), with at least one marker associated with each binary trait locus: 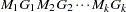. One allele is fixed in backcross populations, so there are 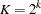unique marker classes or BTL 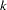-locus genotypes. In an 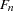population with phase unknown, each locus has three possible genotypes, giving a total of 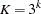genotypes across the 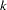markers or BTL. The recombination rate between two loci is the probability that a crossover occurs between the loci, ranging from 0 (complete linkage) to 0.5 (no linkage). 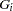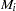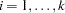This value is represented by for the loci and , , and 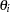for markers 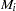and 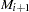, so there are marker recombination parameters. Each penetrance parameter, 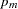, is the probability that a binary trait is present for the 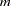th BTL genotype (McIntyre, Coffman, and Doerge 2001). Similarly, 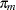denotes the penetrance parameter for the 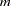th marker genotype.

The joint probabilities of the BTL genotypes (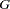), the marker classes (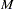), and the trait () can be expressed in matrix form in terms of , , 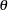and 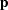, assuming no selection, interference, or mutation, as shown by Simonsen (2004). These probabilities provide a likelihood equation for , , 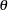and 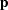. From this likelihood, the maximum likelihood estimate (MLE) for 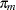, , 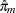is given by the observed binomial proportion of individuals with marker genotype 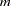in whom the trait is present. The invariance property of MLEs (Casella and Berger 1990) can be applied to obtain the MLE of penetrance parameters 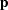as the product of 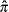and a function of the recombination rates . By entering a known set of or performing a grid search over a range of possible values of , unique estimates of penetrance parameters 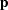can be computed.