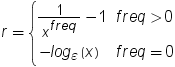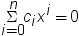The INTRR function returns the internal rate of return over a specified base period of time for the set of cash payments c0, c1, ..., cn. The time intervals between any two consecutive payments are assumed to be equal. The argument freq > 0 describes the number of payments that occur over the specified base period of time. The number of notes issued from each instance is limited.

The internal rate of return is the interest rate such that the sequence of payments has a 0 net present value. (See the NPV Function.) It is given by the following equation.

$table with 1 row and 1 column , row1 column 1 , r equals left brace . table with 2 rows and 2 columns , row1 column 1 , fraction 1 , over x super f r e q end super end fraction . minus 1 , column 2 f r e q greater than 0 , row2 column 1 , negative l o , g sub epsilon . open x close , column 2 f r e q equals 0 , end table , end table$

In this equation, x is the real root of the polynomial.

table with 1 row and 1 column , row1 column 1 , modified cap sigma with i equals 0 below and with n above . c sub i , x to the i , equals 0 , end table

In the case of multiple roots, one real root is returned and a warning is issued concerning the non-uniqueness of the returned internal rate of return. Depending on the value of payments, a root for the equation does not always exist. In that case, a missing value is returned.

Missing values in the payments are treated as 0 values. When freq > 0, the computed rate of return is the effective rate over the specified base period. To compute a quarterly internal rate of return (the base period is three months) with monthly payments, set freq to 3.

If freq is 0, continuous compounding is assumed and the base period is the time interval between two consecutive payments. The computed internal rate of return is the nominal rate of return over the base period. To compute with continuous compounding and monthly payments, set freq to 0. The computed internal rate of return will be a monthly rate.

Comparisons

The IRR function is identical to INTRR, except for in the IRR function, the internal rate of return is a percentage.

Example

For an initial outlay of $400 and expected payments of $100, $200, and $300 over the following three years, the annual internal rate of return can be expressed as

select intrr(1,-400,100,200,300);

The value that is returned is 0.1943770996.

INTRR Function

Syntax

Arguments

freq

c0, c1[ …, cn]

Details

Comparisons

Example

See Also