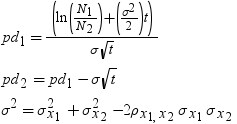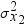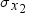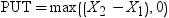MARGRPTPRC Function

Calculates put prices for European options on stocks, based on the Margrabe model.

Category: Financial
Returned data type: DOUBLE
Syntax
Arguments
Details
Comparisons
Example
See Also

Syntax

MARGRPTPRC(X1, t, X2, sigma1, sigma2, rho12)

Arguments

X1

is a nonmissing, positive value that specifies the price of the first asset.

Requirement Specify X1 and X2 in the same units.
Data type DOUBLE

t

is a nonmissing value that specifies the time to expiration, in years.

Data type DOUBLE

X2

is a nonmissing, positive value that specifies the price of the second asset.

Requirement Specify X2 and X1 in the same units.
Data type DOUBLE

sigma1

is a nonmissing, positive fraction that specifies the volatility of the first asset.

Data type DOUBLE

sigma2

is a nonmissing, positive fraction that specifies the volatility of the second asset.

Data type DOUBLE

rho12

specifies the correlation between the first and second assets, 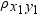rho sub x sub 1 , y sub 1 end sub

Range between –1 and 1
Data type DOUBLE

Details

The MARGRPTPRC function calculates the put price for European options on stocks, based on the Margrabe model. The function is based on the following relationship:
table with 1 row and 1 column , row1 column 1 , p u t , equals , x sub 2 n . open p , d sub 1 , close . minus , x sub 1 n . open p , d sub 2 , close , end table
Arguments
X1
specifies the price of the first asset.
X2
specifies the price of the second asset.
N
specifies the cumulative normal density function.
table with 3 rows and 1 column , row1 column 1 , p , d sub 1 , equals . fraction open natural log of . open . fraction n sub 1 , over n sub 2 end fraction . close . plus . open , fraction sigma squared , over 2 end fraction , close . t close , over sigma square root of t end fraction , row2 column 1 , p , d sub 2 , equals p , d sub 1 , minus sigma square root of t , row3 column 1 , sigma squared , equals . sigma with subscript x sub 1 , and with superscript 2 , end sub-superscript . plus . sigma with subscript x sub 2 , and with superscript 2 , end sub-superscript . negative 2 rho sub x sub 1 comma end sub . x sub 2 end sub . sigma sub x sub 1 end sub . sigma sub x sub 2 end sub , end table
The following arguments apply to the preceding equation:
t
is a nonmissing value that specifies the time to expiration, in years.
sigma with subscript x sub 1 , and with superscript 2 , end sub-superscript
specifies the variance of the first asset.
sigma with subscript x sub 2 , and with superscript 2 , end sub-superscript
specifies the variance of the second asset.
sigma sub x sub 1 end sub
specifies the volatility of the first asset.
sigma sub x sub 2 end sub
specifies the volatility of the second asset.
rho sub x sub 1 comma end sub . x sub 2 end sub
specifies the correlation between the first and second assets.
To view the corresponding CALL relationship, see the MARGRCLPRC Function.
For the special case of t=0, the following equation is true:
table with 1 row and 1 column , row1 column 1 , p u t , equals mehx of . open . open , x sub 2 , minus , x sub 1 , close . comma 0 close , end table
Note: This function assumes that there are no dividends from the two assets.
For information about the basics of pricing, see Using Pricing Functions in SAS Functions and CALL Routines: Reference.

Comparisons

The MARGRPTPRC function calculates the put price for European options on stocks, based on the Margrabe model. The MARGRCLPRC function calculates the call price for European options on stocks, based on the Margrabe model. These functions return a scalar value.

Example

The following statements illustrate the MARGRPTPRC function:
Statements
Results 
select margrptprc(2, .25, 3, .06, .2, 1);
 
1.0000000000973
 
select margrptprc(3, .25, 4, .05, .3, 1);
 
1.00157624907712

See Also

Functions:
MARGRCLPRC Function
Copyright © SAS Institute Inc. All rights reserved.