What’s New in SAS/ETS 14.1

The Hausman and Taylor (1981) and Amemiya and MaCurdy (1986) estimators, which are hybrids that combine the desirable properties of fixed-effects and random-effects models. Under the right circumstances, these estimators afford you the consistency of fixed effects and the efficiency and wider applicability of random effects. Both estimators are instrumental-variables regressions, where you stipulate a set of regressors as correlated with individual effects. The instrumental variables are then determined internally from the set of uncorrelated regressors, their individual-level means, and their deviations from individual-level means. To obtain these estimators, first specify the correlated regressors in the CORRELATED= option in the INSTRUMENTS statement, and then specify the HTAYLOR or AMACURDY option in the MODEL statement.

Comparison tables for multiple models. The new COMPARE statement creates tables of side-by-side comparisons of parameter estimates and other model statistics. You can fit multiple models in the PANEL procedure by issuing multiple MODEL statements. Also specifying a COMPARE statement creates tables that compare the models. The COMPARE statement creates two tables: the first table compares model fit statistics such as 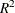and MSE; the second table compares regression coefficients, their standard errors, and (optionally) t tests.

More general Hausman specification tests. In previous versions, Hausman tests for random effects required that the random-effects model contain no time-invariant regressors (regressors that would be dropped from the fixed-effects model). That requirement has been relaxed in SAS/ETS 14.1, and the Hausman test is now a comparison of regressors that are common to both the random- and fixed-effects models. A new column labeled “Coefficients” has been added to the output table for the Hausman test. The “Coefficients” column tells you how many coefficients are common to both models, and thus also tells you the nominal rank of the test.