The MODEL Procedure

Hausman Specification Test

Hausman’s specification test, or m-statistic, can be used to test hypotheses in terms of bias or inconsistency of an estimator. This test was also proposed by Wu (1973). Hausman’s m-statistic is as follows.

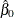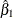Given two estimators, ${\hat{{\beta }}_{0}}$ and ${\hat{{\beta }}_{1}}$ , where under the null hypothesis both estimators are consistent but only 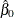${\hat{{\beta }}_{0}}$ is asymptotically efficient and under the alternative hypothesis only 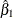${\hat{{\beta }}_{1}}$ is consistent, the m-statistic is

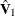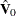$m = {\hat{q}’} (\hat{\mi{\bV } }_{1} - \hat{\mi{\bV } }_{0})^{-}\hat{q}$

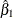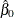where ${\hat{\mi{\bV } }_{1}}$ and ${\hat{\mi{\bV } }_{0}}$ represent consistent estimates of the asymptotic covariance matrices of ${\hat{{\beta }}_{1}}$ and ${\hat{{\beta }}_{0}}$ respectively, and

$q = \hat{{\beta }}_{1} - \hat{{\beta }}_{0}$

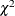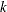The m-statistic is then distributed ${{\chi }^{2}}$ with ${k}$ degrees of freedom, where 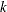${k}$ is the rank of the matrix 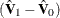${(\hat{\mi{\bV } }_{1} - \hat{\mi{\bV } }_{0})}$ . A generalized inverse is used, as recommended by Hausman and Taylor (1982).

In the MODEL procedure, Hausman’s m-statistic can be used to determine if it is necessary to use an instrumental variables method rather than a more efficient OLS estimation. Hausman’s m-statistic can also be used to compare 2SLS with 3SLS for a class of estimators for which 3SLS is asymptotically efficient (similarly for OLS and SUR).

Hausman’s m-statistic can also be used, in principle, to test the null hypothesis of normality when comparing 3SLS to FIML. Because of the poor performance of this form of the test, it is not offered in the MODEL procedure. See Fair (1984, pp. 246–247) for a discussion of why Hausman’s test fails for common econometric models.

To perform a Hausman’s specification test, specify the HAUSMAN option in the FIT statement. The selected estimation methods are compared using Hausman’s m-statistic.

In the following example, Hausman’s test is used to check the presence of measurement error. Under 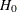${\mi{H}_{0}}$ of no measurement error, OLS is efficient, while under 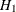${\mi{H}_{1}}$ , 2SLS is consistent. In the following code, OLS and 2SLS are used to estimate the model, and Hausman’s test is requested.

proc model data=one out=fiml2;
   endogenous y1 y2;

   y1 = py2 * y2 + px1 * x1 + interc;
   y2 = py1* y1 + pz1 * z1 + d2;

   fit y1 y2 / ols 2sls hausman;
   instruments x1 z1;
run;

The output specified by the HAUSMAN option produces the results shown in Figure 26.56.

Figure 26.56: Hausman’s Specification Test Results

The MODEL Procedure

Hausman's Specification Test Results
Efficient under H0	Consistent under H1	DF	Statistic	Pr > ChiSq
OLS	2SLS	6	13.86	0.0313

Figure 26.56 indicates that 2SLS is preferred over OLS at 5% level of significance. In this case, the null hypothesis of no measurement error is rejected. Hence, the instrumental variable estimator is required for this example due to the presence of measurement error.