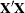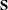The MODEL Procedure
Computer Resource Requirements
If you are estimating large systems, you need to be aware of how PROC MODEL uses computer resources (such as memory and the CPU) so they can be used most efficiently.
Saving Time with Large Data Sets
If your input data set has many observations, the FIT statement performs a large number of model program executions. A pass through the data is made at least once for each iteration and the model program is executed once for each observation in each pass. If you refine the starting estimates by using a smaller data set, the final estimation with the full data set might require fewer iterations.
For example, you could use
proc model;
/* Model goes here */
fit / data=a(obs=25);
fit / data=a;
where OBS=25 selects the first 25 observations in A. The second FIT statement produces the final estimates using the full data set and starting values from the first run.
Fitting the Model in Sections to Save Space and Time
If you have a very large model (with several hundred parameters, for example), the procedure uses considerable space and time. You might be able to save resources by breaking the estimation process into several steps and estimating the parameters in subsets.
You can use the FIT statement to select for estimation only the parameters for selected equations. Do not break the estimation into too many small steps; the total computer time required is minimized by compromising between the number of FIT statements that are executed and the size of the crossproducts matrices that must be processed.
When the parameters are estimated for selected equations, the entire model program must be executed even though only a part of the model program might be needed to compute the residuals for the equations selected for estimation. If the model itself can be broken into sections for estimation (and later combined for simulation and forecasting), then more resources can be saved.
For example, to estimate the following four equation model in two steps, you could use
proc model data=a outmodel=part1;
parms a0-a2 b0-b2 c0-c3 d0-d3;
y1 = a0 + a1*y2 + a2*x1;
y2 = b0 + b1*y1 + b2*x2;
y3 = c0 + c1*y1 + c2*y4 + c3*x3;
y4 = d0 + d1*y1 + d2*y3 + d3*x4;
fit y1 y2;
fit y3 y4;
fit y1 y2 y3 y4;
run;
You should try estimating the model in pieces to save time only if there are more than 14 parameters; the preceding example takes more time, not less, and the difference in memory required is trivial.
Memory Requirements for Parameter Estimation
PROC MODEL is a large program, and it requires much memory. Memory is also required for the SAS System, various data areas, the model program and associated tables and data vectors, and a few crossproducts matrices. For most models, the memory required for PROC MODEL itself is much larger than that required for the model program, and the memory required for the model program is larger than that required for the crossproducts matrices.
The number of bytes needed for two crossproducts matrices, four S matrices, and three parameter covariance matrices is
![\[ 8 \times (2+k+m+g)^{2}+16 \times g^{2 }+12 \times (p+1)^{2} \]](images/etsug_model0290.png)
plus lower-order terms, where m is the number of unique nonzero derivatives of each residual with respect to each parameter, g is the number of equations, k is the number of instruments, and p is the number of parameters. This formula is for the memory required for 3SLS. If you are using OLS, a reasonable estimate of the memory required for large problems (greater than 100 parameters) is to divide the value obtained from the formula in half.
Consider the following model program.
proc model data=test2 details; exogenous x1 x2; parms b1 100 a1 a2 b2 2.5 c2 55; y1 = a1 * y2 + b1 * x1 * x1; y2 = a2 * y1 + b2 * x2 * x2 + c2 / x2; fit y1 y2 / n3sls memoryuse; inst b1 b2 c2 x1 ; run;
The DETAILS option prints the storage requirements information shown in Figure 26.38.
Figure 26.38: Storage Requirements Information
The matrix 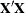 augmented by the residual vector is called the XPX matrix in the output, and it has the size
augmented by the residual vector is called the XPX matrix in the output, and it has the size 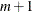 . The order of the S matrix, 2 for this example, is the value of g. The CROSS matrix is made up of the k unique instruments, a constant column that represents the intercept terms, followed by the m unique Jacobian variables plus a constant column that represents the parameters with constant derivatives, followed by the
g residuals.
. The order of the S matrix, 2 for this example, is the value of g. The CROSS matrix is made up of the k unique instruments, a constant column that represents the intercept terms, followed by the m unique Jacobian variables plus a constant column that represents the parameters with constant derivatives, followed by the
g residuals.
The size of two CROSS matrices in bytes is
![\[ 8 \times (2+k+m+g)^{2}+2+k+m+g \]](images/etsug_model0292.png)
Note that the CROSS matrix is symmetric, so only the diagonal and the upper triangular part of the matrix is stored. For examples of the CROSS and XPX matrices see the section Iteration History.
The MEMORYUSE Option
The MEMORYUSE option in the FIT, SOLVE, MODEL, or RESET statement can be used to request a comprehensive memory usage summary.
Figure 26.39 shows an example of the output produced by the MEMORYUSE option.
Figure 26.39: MEMORYUSE Option Output for FIT Task
| Memory Usage Summary (in bytes) | |
|---|---|
| Symbols | 17060 |
| Strings | 2593 |
| Lists | 2428 |
| Arrays | 2300 |
| Statements | 2704 |
| Opcodes | 1840 |
| Parsing | 6180 |
| Executable | 12845 |
| Block option | 0 |
| Cross reference | 0 |
| Flow analysis | 336 |
| Derivatives | 28640 |
| Data vector | 368 |
| Cross matrix | 1480 |
| X'X matrix | 590 |
| S matrix | 144 |
| GMM memory | 0 |
| Jacobian | 0 |
| Work vectors | 702 |
| Overhead | 14246 |
| ----------------------- | -------------- |
| Total | 94456 |
Definitions of the memory components follow:
|
symbols |
memory used to store information about variables in the model |
|
strings |
memory used to store the variable names and labels |
|
lists |
space used to hold lists of variables |
|
arrays |
memory used by ARRAY statements |
|
statements |
memory used for the list of programming statements in the model |
|
opcodes |
memory used to store the code compiled to evaluate the |
|
expression in the model program |
|
|
parsing |
memory used in parsing the SAS statements |
|
executable |
the compiled model program size |
|
block option |
memory used by the BLOCK option |
|
cross ref. |
memory used by the XREF option |
|
flow analysis |
memory used to compute the interdependencies of the variables |
|
derivatives |
memory used to compute and store the analytical derivatives |
|
data vector |
memory used for the program data vector |
|
cross matrix |
memory used for one or more copies of the CROSS matrix |
|
|
memory used for one or more copies of the |
|
|
memory used for the covariance matrix |
|
GMM memory |
additional memory used for the GMM and ITGMM methods |
|
Jacobian |
memory used for the Jacobian matrix for SOLVE and FIML |
|
work vectors |
memory used for miscellaneous work vectors |
|
overhead |
other miscellaneous memory |