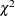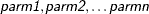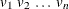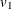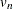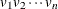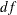The MODEL Procedure

ERRORMODEL Statement

Subsections:

  • ERRORMODEL equation-name $\sim $ distribution < CDF= CDF(options) > ;

The ERRORMODEL statement is the mechanism for specifying the distribution of the residuals. You must specify the dependent/endogenous variables or general form model name, a tilde (~), and then a distribution with its parameters. You can specify the following options:

Options to Specify the Distribution

CAUCHY( <location, scale> )

specifies the Cauchy distribution. This option is supported only for simulation. The arguments correspond to the arguments of the SAS CDF function that computes the cumulative distribution function (ignoring the random variable argument).

CHISQUARED ( df <, nc> )

specifies the 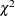$\chi ^2$ distribution. This option is supported only for simulation. The arguments correspond to the arguments of the SAS CDF function (ignoring the random variable argument).

GENERAL(Likelihood <, parm1, parm2, $\dots $ parmn > )

specifies the negative of a general log-likelihood function that you construct by using SAS programming statements. The procedure minimizes the negative log-likelihood function specified. 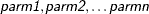$\Argument{parm1}, \Argument{parm2}, \ldots \Argument{parmn}$ are optional parameters for this distribution and are used for documentation purposes only.

F( ndf, ddf <, nc> )

specifies the F distribution. This option is supported only for simulation. The arguments correspond to the arguments of the SAS CDF function (ignoring the random variable argument).

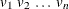NORMAL( $v_1\ v_2\ \ldots \ v_ n$ )

specifies a multivariate normal (Gaussian) distribution with mean 0 and variances 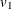$v_1$ through $v_ n$.

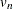POISSON( mean )

specifies the Poisson distribution. This option is supported only for simulation. The arguments correspond to the arguments of the SAS CDF function (ignoring the random variable argument).

T( 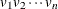$v_1 v_2 \cdots v_ n$, df )

specifies a multivariate t distribution with noncentrality 0, variance 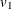$v_1$ through 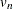$v_ n$, and common degrees of freedom $df$.

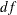UNIFORM( <left, right> )

specifies the uniform distribution. This option is supported only for simulation. The arguments correspond to the arguments of the SAS CDF function (ignoring the random variable argument).

Options to Specify the CDF for Simulation

CDF=( CDF(options) )

specifies the univariate distribution that is used for simulation so that the estimation can be done for one set of distributional assumptions and the simulation for another. The CDF can be any of the distributions from the previous section with the exception of the general likelihood. In addition, you can specify the empirical distribution of the residuals.

EMPIRICAL= ( <TAILS=(options)> )

uses the sorted residual data to create an empirical CDF.

TAILS=( tail-options )

specifies how to handle the tails in computing the inverse CDF from an empirical distribution, where tail-options are:

NORMAL

specifies the normal distribution to extrapolate the tails.

T( df )

specifies the t distribution to extrapolate the tails.

PERCENT= p

specifies the percentage of the observations to use in constructing each tail. The default for the PERCENT= option is 10. A normal distribution or a t distribution is used to extrapolate the tails to infinity. The variance for the tail distribution is obtained from the data so that the empirical CDF is continuous.