The MDC Procedure
Multivariate Normal Utility Function
Consider the random utility function
![\[ U_{ij} = \mr{\Variable{ttime} }_{ij}\beta + \epsilon _{ij},\; \; j=1,2,3 \]](images/etsug_mdc0019.png)
where
![\[ \left[ \begin{array}{c}\epsilon _{i1} \\ \epsilon _{i2} \\ \epsilon _{i3} \\ \end{array} \right] \sim N \left( \mathbf{0} ,\left[ \begin{array}{ccc} 1 & \rho _{21} & 0 \\ \rho _{21} & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \right) \]](images/etsug_mdc0020.png)
The correlation coefficient (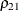
) between 
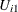and 
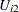represents commonly neglected attributes of public transportation modes, 1 and 2. The following SAS statements estimate this
trinomial probit model:
/*-- homoscedastic mprobit --*/
proc mdc data=newdata;
model decision = ttime /
type=mprobit
nchoice=3
unitvariance=(1 2 3)
covest=hess;
id pid;
run;
The UNITVARIANCE=(1 2 3) option specifies that the random component of utility for each of these choices has unit variance.
If the UNITVARIANCE= option is specified, it needs to include at least two choices. The results of this constrained multinomial
probit model estimation are displayed in Figure 25.12 and Figure 25.13. The test for ttime = 0 is rejected at the 1% significance level.
Figure 25.12: Constrained Probit Estimation Summary
| Model Fit Summary | |
|---|---|
| Dependent Variable | decision |
| Number of Observations | 50 |
| Number of Cases | 150 |
| Log Likelihood | -33.88604 |
| Log Likelihood Null (LogL(0)) | -54.93061 |
| Maximum Absolute Gradient | 0.0002380 |
| Number of Iterations | 8 |
| Optimization Method | Dual Quasi-Newton |
| AIC | 71.77209 |
| Schwarz Criterion | 75.59613 |
| Number of Simulations | 100 |
| Starting Point of Halton Sequence | 11 |
Figure 25.13: Multinomial Probit Estimates with Unit Variances