Using Predictor Variables
A Seasonal Dummies predictor is a special feature that adds to the model seasonal indicator or "dummy" variables to serve as regressors for seasonal effects.
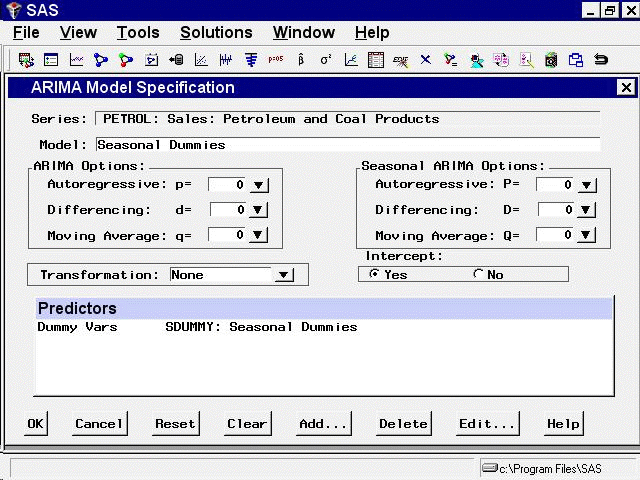
From the Develop Models window, select Fit ARIMA Model. From the ARIMA Model Specification window, select Add and then select Seasonal Dummies from the menu (shown in Figure 50.1).
A Seasonal Dummies input is added to the Predictors list, as shown in Figure 50.24.
Select the OK button. A model consisting of an intercept and 11 seasonal dummy variables is fit and added to the model list in the Develop
Models window. This is effectively a mean model with a separate mean for each month.
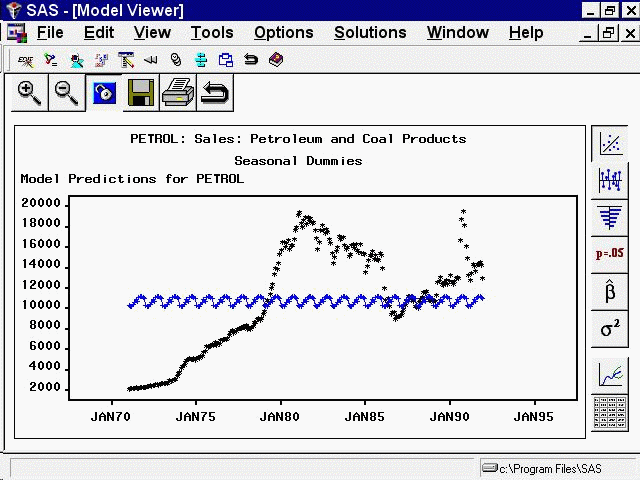
Now return to the Model Viewer, which displays a plot of the model predictions and actual series values, as shown in Figure 50.25. This is obviously a poor model for this series, but it serves to illustrate how seasonal dummy variables work.
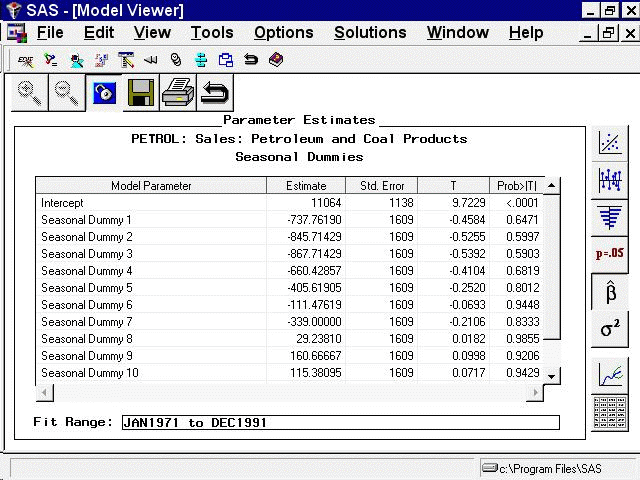
Now select the parameter estimates icon, the fifth from the top on the vertical toolbar. This displays the Parameter Estimates table, as shown in Figure 50.26.
Since the data for this example are monthly, the Seasonal Dummies option added 11 seasonal dummy variables. These include a dummy regressor variable that is 1.0 for January and 0 for other months, a regressor that is 1.0 only for February, and so forth through November.
Because the model includes an intercept, no dummy variable is added for December. The December effect is measured by the intercept, while the effect of other seasons is measured by the difference between the intercept and the estimated regression coefficient for the season’s dummy variable.
The same principle applies for other data frequencies: the "Seasonal Dummy 1" parameter always refers to the first period in the seasonal cycle; and, when an intercept is present in the model, there is no seasonal dummy parameter for the last period in the seasonal cycle.