The MODEL Procedure
In this example a nonlinear model is estimated by using the Cauchy distribution. Then a simulation is done for one observation in the data.
The following DATA step creates the data for the model.
/* Generate a Cauchy distributed Y */
data c;
format date monyy.;
call streaminit(156789);
do t=0 to 20 by 0.1;
date=intnx('month','01jun90'd,(t*10)-1);
x=rand('normal');
e=rand('cauchy') + 10 ;
y=exp(4*x)+e;
output;
end;
run;
The model to be estimated is
That is, the residuals of the model are distributed as a Cauchy distribution with noncentrality parameter ![]() .
.
The log likelihood for the Cauchy distribution is
The following SAS statements specify the model and the log-likelihood function.
title1 'Cauchy Distribution';
proc model data=c ;
dependent y;
parm a -2 nc 4;
y=exp(-a*x);
/* Likelihood function for the residuals */
obj = log(constant('pi')*(1+(-resid.y-nc)**2));
errormodel y ~ general(obj) cdf=cauchy(nc);
fit y / outsn=s1 method=marquardt;
solve y / sdata=s1 data=c(obs=1) random=1000
seed=256789 out=out1;
run;
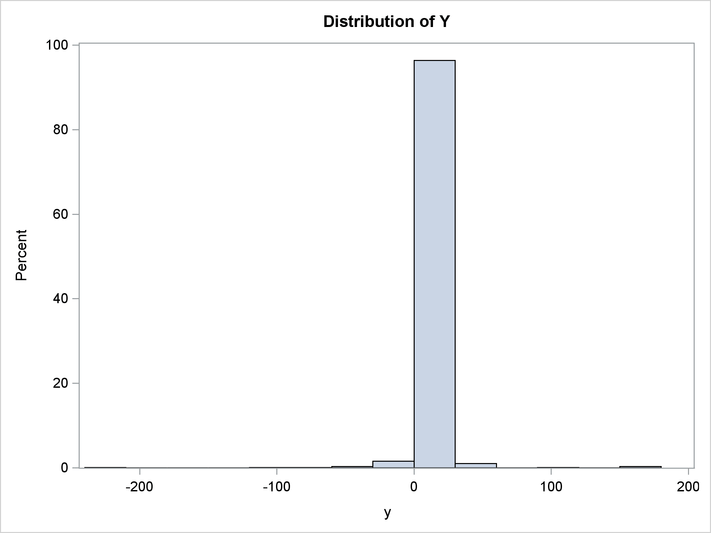
title 'Distribution of Y';
proc sgplot data=out1;
histogram y;
run;
The FIT statement uses the OUTSN= option to output the ![]() matrix for residuals from the normal distribution. The
matrix for residuals from the normal distribution. The ![]() matrix is
matrix is ![]() and has value 1.0 because it is a correlation matrix. The OUTS= matrix is the scalar 2989.0. Because the distribution is
univariate (no covariances), the OUTS= option would produce the same simulation results. The simulation is performed by using
the SOLVE statement.
and has value 1.0 because it is a correlation matrix. The OUTS= matrix is the scalar 2989.0. Because the distribution is
univariate (no covariances), the OUTS= option would produce the same simulation results. The simulation is performed by using
the SOLVE statement.
The distribution of y is shown in the following output.