The MODEL Procedure
This example illustrates the use of the MODEL procedure for nonlinear ordinary least squares (OLS) regression. The model is a logistic growth curve for the population of the United States. The data is the population in millions recorded at ten-year intervals starting in 1790 and ending in 2000. For an explanation of the starting values given by the START= option, see the section Troubleshooting Convergence Problems. Portions of the output from the following statements are shown in Output 19.1.1 through Output 19.1.3.
title 'Logistic Growth Curve Model of U.S. Population'; data uspop; input pop :6.3 @@; retain year 1780; year=year+10; label pop='U.S. Population in Millions'; datalines; 3929 5308 7239 9638 12866 17069 23191 31443 39818 50155 62947 75994 91972 105710 122775 131669 151325 179323 203211 226542 248710 ;
proc model data=uspop;
label a = 'Maximum Population'
b = 'Location Parameter'
c = 'Initial Growth Rate';
pop = a / ( 1 + exp( b - c * (year-1790) ) );
fit pop start=(a 1000 b 5.5 c .02) / out=resid outresid;
run;
The adjusted ![]() value indicates the model fits the data well. There are only 21 observations and the model is nonlinear, so significance
tests on the parameters are only approximate. The significance tests and associated approximate probabilities indicate that
all the parameters are significantly different from 0.
value indicates the model fits the data well. There are only 21 observations and the model is nonlinear, so significance
tests on the parameters are only approximate. The significance tests and associated approximate probabilities indicate that
all the parameters are significantly different from 0.
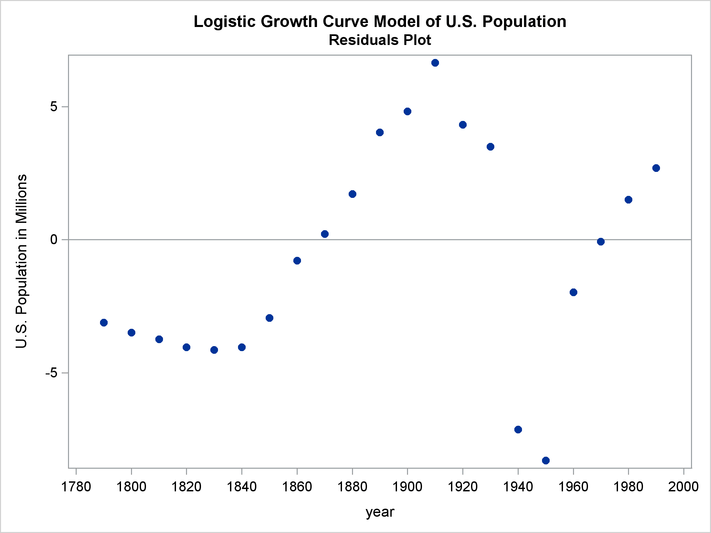
The FIT statement included the options OUT=RESID and OUTRESID so that the residuals from the estimation are saved to the data set RESID. The residuals are plotted to check for heteroscedasticity by using PROC SGPLOT as follows.
title2 "Residuals Plot"; proc sgplot data=resid; refline 0; scatter x=year y=pop / markerattrs=(symbol=circlefilled); xaxis values=(1780 to 2000 by 20); run;
The plot is shown in Output 19.1.4.
The residuals do not appear to be independent, and the model could be modified to explain the remaining nonrandom errors.