The MODEL Procedure

Solution Mode Output

Subsections:

Summary Statistics

The following SAS statements dynamically forecast the solution to a nonlinear equation:

proc model data=sashelp.citimon;
   parameters a 0.010708  b  -0.478849 c 0.929304;
   lhur = 1/(a * ip) + b + c * lag(lhur);
   solve lhur / out=sim forecast dynamic;
run;

The first page of output produced by the SOLVE step is shown in Figure 19.77. This is the summary description of the model. The error message states that the simulation was aborted at observation 144 because of missing input values.

Figure 19.77: Solve Step Summary Output

The MODEL Procedure

Model Summary
Model Variables	1
Parameters	3
Equations	1
Number of Statements	1
Program Lag Length	1

Model Variables	LHUR
Parameters(Value)	a(0.010708) b(-0.478849) c(0.929304)
Equations	LHUR

The second page of output, shown in Figure 19.78, gives more information on the failed observation.

Figure 19.78: Solve Step Error Message

The MODEL Procedure

Dynamic Single-Equation Forecast

Solution values are missing because of missing input values for observation 144 at NEWTON iteration 0.

Note:

Additional information on the values of the variables at this observation, which may be helpful in determining the cause of the failure of the solution process, is printed below.

Observation	144	Iteration	0	CC	-1.000000
		Missing	1

Iteration Errors - Missing.

                              The MODEL Procedure                               
                        Dynamic Single-Equation Forecast                        
                                                                                
                     --- Listing of Program Data Vector ---                     
_N_:                144     ACTUAL.LHUR:          .     ERROR.LHUR:           . 
IP:                   .     LHUR:           7.10000     PRED.LHUR:            . 
a:              0.01071     b:             -0.47885     c:              0.92930

Note:

Simulation aborted.

From the program data vector, you can see the variable IP is missing for observation 144. LHUR could not be computed, so the simulation aborted.

The solution summary table is shown in Figure 19.79.

Figure 19.79: Solution Summary Report

The MODEL Procedure

Dynamic Single-Equation Forecast

Data Set Options
DATA=	SASHELP.CITIMON
OUT=	SIM

Solution Summary
Variables Solved	1
Forecast Lag Length	1
Solution Method	NEWTON
CONVERGE=	1E-8
Maximum CC	0
Maximum Iterations	1
Total Iterations	143
Average Iterations	1

Observations Processed
Read	145
Lagged	1
Solved	143
First	2
Last	145
Failed	1

Variables Solved For	LHUR

This solution summary table includes the names of the input data set and the output data set followed by a description of the model. The table also indicates that the solution method defaulted to Newton’s method. The remaining output is defined as follows.

Maximum CC	is the maximum convergence value accepted by the Newton
	procedure. This number is always less than the value
	for the CONVERGE= option.
Maximum Iterations	is the maximum number of Newton iterations performed
	at each observation and each replication of Monte
	Carlo simulations.
Total Iterations	is the sum of the number of iterations required for each
	observation and each Monte Carlo simulation.
Average Iterations	is the average number of Newton iterations required to
	solve the system at each step.
Solved	is the number of observations used times the number of
	random replications selected plus one, for Monte Carlo
	simulations. The one additional simulation is the original
	unperturbed solution. For simulations that do not involve Monte
	Carlo, this number is the number of observations used.

Summary Statistics

The STATS and THEIL options are used to select goodness-of-fit statistics. Actual values must be provided in the input data set for these statistics to be printed. When the RANDOM= option is specified, the statistics do not include the unperturbed (_REP_=0) solution.

STATS Option Output

The following statements show the addition of the STATS and THEIL options to the model in the previous section:

proc model data=sashelp.citimon;
   parameters a 0.010708  b  -0.478849 c 0.929304;
   lhur= 1/(a * ip) + b + c * lag(lhur) ;
   solve lhur / out=sim dynamic stats theil;
   range date to '01nov91'd;
run;

The STATS output in Figure 19.80 and the THEIL output in Figure 19.81 are generated.

Figure 19.80: STATS Output

The MODEL Procedure

Dynamic Single-Equation Simulation

Solution Range DATE = FEB1980 To NOV1991

Descriptive Statistics
Variable	N Obs	N	Actual		Predicted		Label
Variable	N Obs	N	Mean	Std Dev	Mean	Std Dev	Label
LHUR	142	142	7.0887	1.4509	7.2473	1.1465	UNEMPLOYMENT RATE: ALL WORKERS, 16 YEARS

Statistics of fit
Variable	N	Mean Error	Mean % Error	Mean Abs Error	Mean Abs % Error	RMS Error	RMS % Error	R-Square	Label
LHUR	142	0.1585	3.5289	0.6937	10.0001	0.7854	11.2452	0.7049	UNEMPLOYMENT RATE: ALL WORKERS, 16 YEARS

The number of observations (Nobs), the number of observations with both predicted and actual values nonmissing (N), and the mean and standard deviation of the actual and predicted values of the determined variables are printed first. The next set of columns in the output are defined as follows:

Mean Error	${\frac{1}{N}\sum _{j=1}^{N}{(\hat{y}_{j} - y_{j} )}}$
Mean % Error	${\frac{100}{N}\sum _{j=1}^{N}{(\hat{y}_{j} - y_{j}) / y_{j}}}$
Mean Abs Error	${\frac{1}{N}\sum _{j=1}^{N}{\|{\hat{y}_{j} - y_{j} }\|}}$
Mean Abs % Error	${\frac{100}{N}\sum _{j=1}^{N}{{\|(\hat{y}_{j} - y_{j})/ y_{j}\|}}}$
RMS Error	${\sqrt {\frac{1}{N}\sum _{j=1}^{N}{(\hat{y}_{j} - y_{j})^{2}}}}$
RMS % Error	${100\sqrt {\frac{1}{N}\sum _{j=1}^{N}{((\hat{y}_{j} - y_{j})/ y_{j})^{2}}}}$
R-square	${1 - \mi{SSE} / \mi{CSSA}}$
SSE	${\sum _{j=1}^{N}{(\hat{y}_{j} - y_{j} )^{2}}}$
SSA	${\sum _{j=1}^{N}{(y_{j} )^{2}}}$
CSSA	${\mi{SSA} - \left(\sum _{j=1}^{N}{y_{j}} \right)^{2}}$
$\hat{y}$	predicted value
y	actual value

When the RANDOM= option is specified, the statistics do not include the unperturbed (_REP_=0) solution.

THEIL Option Output

The THEIL option specifies that Theil forecast error statistics be computed for the actual and predicted values and for the relative changes from lagged values. Mathematically, the quantities are

$\hat{yc} = (\hat{y} - lag(y)) / lag(y)$

$yc = (y - lag(y)) / lag(y)$

where $\hat{yc}$ is the relative change for the predicted value and $yc$ is the relative change for the actual value.

Figure 19.81: THEIL Output

Theil Forecast Error Statistics
Variable	N	MSE	Corr (R)	MSE Decomposition Proportions					Inequality Coef		Label
Variable	N	MSE	Corr (R)	Bias (UM)	Reg (UR)	Dist (UD)	Var (US)	Covar (UC)	U1	U	Label
LHUR	142	0.6168	0.85	0.04	0.01	0.95	0.15	0.81	0.1086	0.0539	UNEMPLOYMENT RATE: ALL WORKERS, 16 YEARS

Theil Relative Change Forecast Error Statistics
Variable	Relative Change			MSE Decomposition Proportions					Inequality Coef		Label
Variable	N	MSE	Corr (R)	Bias (UM)	Reg (UR)	Dist (UD)	Var (US)	Covar (UC)	U1	U	Label
LHUR	142	0.0126	-0.08	0.09	0.85	0.06	0.43	0.47	4.1226	0.8348	UNEMPLOYMENT RATE: ALL WORKERS, 16 YEARS

The columns have the following meaning:

Corr (R)

is the correlation coefficient, 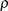${{\rho }}$ , between the actual and predicted values.

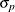${\rho } = \frac{\mr{cov}( y, \hat{y})}{ {\sigma }_{a} {\sigma }_{p}}$

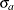where ${{\sigma }_{p}}$ and ${{\sigma }_{a}}$ are the standard deviations of the predicted and actual values.

Bias (UM)

is an indication of systematic error and measures the extent to which the average values of the actual and predicted deviate from each other.

$\frac{(\mr{E}(y)- \mr{E}(\hat{y}))^{2}}{ \frac{1}{N} \sum _{t=1}^{N}{(y_{t} - \hat{y}_{t})^{2}}}$

Reg (UR)

is defined as 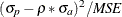${({\sigma }_{p} - {\rho } * {\sigma }_{a})^{2}/ \mi{MSE}}$ . Consider the regression

$y = {\alpha }+ {\beta }\hat{y}$

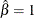If ${\hat{{\beta }}=1}$ , UR will equal zero.

Dist (UD)

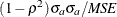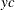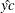is defined as ${(1 - {\rho }^{2}) {\sigma }_{a}{\sigma }_{a}/\mi{MSE} }$ and represents the variance of the residuals obtained by regressing $yc$ on $\hat{yc}$ .

Var (US)

is the variance proportion. US indicates the ability of the model to replicate the degree of variability in the endogenous variable.

$\mi{US} = \frac{({\sigma }_{p}-{\sigma }_{a})^{2}}{\mi{MSE}}$

Covar (UC)

represents the remaining error after deviations from average values and average variabilities have been accounted for.

$\mi{UC} = \frac{2(1 - {\rho }) {\sigma }_{p}{\sigma }_{a}}{\mi{MSE}}$

U1

is a statistic that measures the accuracy of a forecast defined as follows:

$\mi{U1} =\frac{\sqrt {\mi{MSE}}}{\sqrt {\frac{1}{N}\sum _{t=1}^{N}{(y_{t})^{2}}}}$

U

is the Theil’s inequality coefficient defined as follows:

$\mi{U} = \frac{\sqrt {\mi{MSE}}}{\sqrt {\frac{1}{N}\sum _{t=1}^{N}{(y_{t})^{2}}} + \sqrt {\frac{1}{N}\sum _{t=1}^{N}{( \hat{y}_{t})^{2}}}}$

MSE

is the mean square error. In the case of the relative change Theil statistics, the MSE is computed as follows:

$\mi{MSE} = \frac{1}{N} \sum _{t=1}^{N}{(\hat{yc}_ t - yc_ t)^{2}}$

More information about these statistics can be found in the references Maddala (1977, pp. 344–347) and Pindyck and Rubinfeld (1981, pp. 364–365).