The MODEL Procedure
The NORMAL option in the FIT statement performs multivariate and univariate tests of normality.
The three multivariate tests provided are Mardia’s skewness test and kurtosis test (Mardia, 1970) and the Henze-Zirkler ![]() test (Henze and Zirkler, 1990). The two univariate tests provided are the Shapiro-Wilk W test and the Kolmogorov-Smirnov test. (For details on the univariate
tests, refer to "Goodness-of-Fit Tests" section in "The UNIVARIATE Procedure" chapter in the Base SAS Procedures Guide.) The null hypothesis for all these tests is that the residuals are normally distributed.
test (Henze and Zirkler, 1990). The two univariate tests provided are the Shapiro-Wilk W test and the Kolmogorov-Smirnov test. (For details on the univariate
tests, refer to "Goodness-of-Fit Tests" section in "The UNIVARIATE Procedure" chapter in the Base SAS Procedures Guide.) The null hypothesis for all these tests is that the residuals are normally distributed.
For a random sample ![]() ,
, ![]() , where d is the dimension of
, where d is the dimension of ![]() and n is the number of observations, a measure of multivariate skewness is
and n is the number of observations, a measure of multivariate skewness is
where S is the sample covariance matrix of X. For weighted regression, both S and ![]() are computed by using the weights supplied by the WEIGHT statement or the _WEIGHT_ variable.
are computed by using the weights supplied by the WEIGHT statement or the _WEIGHT_ variable.
Mardia showed that under the null hypothesis ![]() is asymptotically distributed as
is asymptotically distributed as ![]() . For small samples, Mardia’s skewness test statistic is calculated with a small sample correction formula, given by
. For small samples, Mardia’s skewness test statistic is calculated with a small sample correction formula, given by ![]() where the correction factor k is given by
where the correction factor k is given by ![]() . Mardia’s skewness test statistic in PROC MODEL uses this small sample corrected formula.
. Mardia’s skewness test statistic in PROC MODEL uses this small sample corrected formula.
A measure of multivariate kurtosis is given by
Mardia showed that under the null hypothesis, ![]() is asymptotically normally distributed with mean
is asymptotically normally distributed with mean ![]() and variance
and variance ![]() .
.
The Henze-Zirkler test is based on a nonnegative functional ![]() that measures the distance between two distribution functions and has the property that
that measures the distance between two distribution functions and has the property that
if and only if
where ![]() is a d-dimensional normal distribution.
is a d-dimensional normal distribution.
The distance measure ![]() can be written as
can be written as
where ![]() and
and ![]() are the Fourier transforms of P and Q, and
are the Fourier transforms of P and Q, and ![]() is a weight or a kernel function. The density of the normal distribution
is a weight or a kernel function. The density of the normal distribution ![]() is used as
is used as ![]()
where ![]() .
.
The parameter ![]() depends on
depends on ![]() as
as
The test statistic computed is called ![]() and is approximately distributed as a lognormal. The lognormal distribution is used to compute the null hypothesis probability.
and is approximately distributed as a lognormal. The lognormal distribution is used to compute the null hypothesis probability.
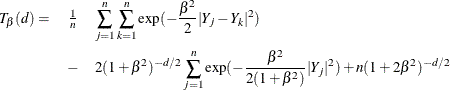
where
Monte Carlo simulations suggest that ![]() has good power against distributions with heavy tails.
has good power against distributions with heavy tails.
The Shapiro-Wilk W test is computed only when the number of observations (n ) is less than 2000 while computation of the Kolmogorov-Smirnov test statistic requires at least 2000 observations.
The following is an example of the output produced by the NORMAL option.
proc model data=test2; y1 = a1 * x2 * x2 - exp( d1*x1); y2 = a2 * x1 * x1 + b2 * exp( d2*x2); fit y1 y2 / normal ; run;