The MDC Procedure
In general, the hypothesis to be tested can be written as
where ![]() is an r-by-1 vector-valued function of the parameters
is an r-by-1 vector-valued function of the parameters ![]() given by the r expressions specified in the TEST statement.
given by the r expressions specified in the TEST statement.
Let ![]() be the estimate of the covariance matrix of
be the estimate of the covariance matrix of ![]() . Let
. Let ![]() be the unconstrained estimate of
be the unconstrained estimate of ![]() and
and ![]() be the constrained estimate of
be the constrained estimate of ![]() such that
such that ![]() . Let
. Let
Using this notation, the test statistics for the three kinds of tests are computed as follows:
-
The Wald test statistic is defined as
![\[ W = h^{'}(\hat{\theta })\big \lgroup { {A(\hat{\theta }) \hat{V} A^{'} (\hat{\theta })} }\big \rgroup ^{-1} h(\hat{\theta }) \]](images/etsug_mdc0208.png)
The Wald test is not invariant to reparameterization of the model (Gregory and Veall 1985; Gallant 1987, p. 219). For more information about the theoretical properties of the Wald test, see Phillips and Park (1988).
-
The Lagrange multiplier test statistic is
![\[ LM = {\lambda }^{'} A(\tilde{\theta }) \tilde{V} A^{'}(\tilde{\theta }) {\lambda } \]](images/etsug_mdc0209.png)
where
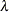 is the vector of Lagrange multipliers from the computation of the restricted estimate
is the vector of Lagrange multipliers from the computation of the restricted estimate 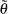 .
.
-
The likelihood ratio test statistic is
![\[ LR = 2 \left({L(\hat{\theta }) - L(\tilde{\theta })}\right) \]](images/etsug_mdc0211.png)
where
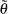 represents the constrained estimate of
represents the constrained estimate of 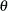 and
and 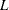 is the concentrated log-likelihood value.
is the concentrated log-likelihood value.
For each kind of test, under the null hypothesis the test statistic is asymptotically distributed as a ![]() random variable with r degrees of freedom, where r is the number of expressions in the TEST statement. The p-values reported for the tests are computed from the
random variable with r degrees of freedom, where r is the number of expressions in the TEST statement. The p-values reported for the tests are computed from the ![]() distribution and are only asymptotically valid.
distribution and are only asymptotically valid.
Monte Carlo simulations suggest that the asymptotic distribution of the Wald test is a poorer approximation to its small sample
distribution than that of the other two tests. However, the Wald test has the lowest computational cost, since it does not
require computation of the constrained estimate ![]() .
.
The following statements are an example of using the TEST statement to perform a likelihood ratio test:
proc mdc;
model decision = x1 x2 / type=clogit
choice=(mode 1 2 3);
id pid;
test 0.5 * x1 + 2 * x2 = 0 / lr;
run;