SAS Macros and Functions

BOXCOXAR Macro

Subsections:

The %BOXCOXAR macro finds the optimal Box-Cox transformation for a time series.

Transformations of the dependent variable are a useful way of dealing with nonlinear relationships or heteroscedasticity. For example, the logarithmic transformation is often used for modeling and forecasting time series that show exponential growth or that show variability proportional to the level of the series.

The Box-Cox transformation is a general class of power transformations that include the log transformation and no transformation as special cases. The Box-Cox transformation is

\begin{eqnarray*} Y_{t} = \begin{cases} \frac{(X_{t}+c)^{{\lambda }}-1}{{\lambda }} & \textrm{for } \lambda \neq 0 \\ {\ln }(X_{t}+c) & \textrm{for } \lambda =0 \end{cases} \nonumber \end{eqnarray*}

The parameter ${\lambda }$ controls the shape of the transformation. For example, ${\lambda }$=0 produces a log transformation, while ${\lambda }$=0.5 results in a square root transformation. When ${\lambda }$=1, the transformed series differs from the original series by ${c-1}$.

The constant c is optional. It can be used when some ${X_{t}}$ values are negative or 0. You choose c so that the series ${X_{t}}$ is always greater than ${- c}$.

The %BOXCOXAR macro tries a range of ${\lambda }$ values and reports which of the values tried produces the optimal Box-Cox transformation. To evaluate different ${\lambda }$ values, the %BOXCOXAR macro transforms the series with each ${\lambda }$ value and fits an autoregressive model to the transformed series. It is assumed that this autoregressive model is a reasonably good approximation to the true time series model appropriate for the transformed series. The likelihood of the data under each autoregressive model is computed, and the ${\lambda }$ value that produces the maximum likelihood over the values tried is reported as the optimal Box-Cox transformation for the series.

The %BOXCOXAR macro prints and optionally writes to a SAS data set all of the ${\lambda }$ values tried, the corresponding log-likelihood value, and related statistics for the autoregressive model.

You can control the range and number of ${\lambda }$ values tried. You can also control the order of the autoregressive models fit to the transformed series. You can difference the transformed series before the autoregressive model is fit.

Note that the Box-Cox transformation might be appropriate when the data have a common distribution (apart from heteroscedasticity) but not when groups of observations for the variable are quite different. Thus the %BOXCOXAR macro is more often appropriate for time series data than for cross-sectional data.

Syntax

The form of the %BOXCOXAR macro is

  • %BOXCOXAR ( SAS-data-set, variable < , options > );

The first argument, SAS-data-set, specifies the name of the SAS data set that contains the time series to be analyzed. The second argument, variable, specifies the time series variable name to be analyzed. The first two arguments are required.

The following options can be used with the %BOXCOXAR macro. Options must follow the required arguments and are separated by commas.

AR=n

specifies the order of the autoregressive model fit to the transformed series. The default is AR=5.

CONST=value

specifies a constant c to be added to the series before transformation. Use the CONST= option when some values of the series are 0 or negative. The default is CONST=0.

DIF=( differencing-list )

specifies the degrees of differencing to apply to the transformed series before the autoregressive model is fit. The differencing-list is a list of positive integers separated by commas and enclosed in parentheses. For example, DIF=(1,12) specifies that the transformed series be differenced once at lag 1 and once at lag 12. For more details, see the section IDENTIFY Statement in Chapter 7: The ARIMA Procedure.

LAMBDAHI=value

specifies the maximum value of lambda for the grid search. The default is LAMBDAHI=1. A large (in magnitude) LAMBDAHI= value can result in problems with floating point arithmetic.

LAMBDALO=value

specifies the minimum value of lambda for the grid search. The default is LAMBDALO=0. A large (in magnitude) LAMBDALO= value can result in problems with floating point arithmetic.

NLAMBDA=value

specifies the number of lambda values considered, including the LAMBDALO= and LAMBDAHI= option values. The default is NLAMBDA=2.

OUT=SAS-data-set

writes the results to an output data set. The output data set includes the lambda values tried (LAMBDA), and for each lambda value, the log likelihood (LOGLIK), residual mean squared error (RMSE), Akaike Information Criterion (AIC), and Schwarz’s Bayesian Criterion (SBC).

PRINT=YES | NO

specifies whether results are printed. The default is PRINT=YES. The printed output contains the lambda values, log likelihoods, residual mean square errors, Akaike Information Criterion (AIC), and Schwarz’s Bayesian Criterion (SBC).

Results

The value of $\lambda $ that produces the maximum log likelihood is returned in the macro variable &BOXCOXAR. The value of the variable &BOXCOXAR is "ERROR" if the %BOXCOXAR macro is unable to compute the best transformation due to errors. This might be the result of large lambda values. The Box-Cox transformation parameter involves exponentiation of the data, so that large lambda values can cause floating-point overflow.

Results are printed unless the PRINT=NO option is specified. Results are also stored in SAS data sets when the OUT= option is specified.

Details

Assume that the transformed series ${Y_{t}}$ is a stationary pth order autoregressive process generated by independent normally distributed innovations.

\[ (1 - {\Theta }({B}))(Y_{t} - {\mu }) = {\epsilon }_{t} \]
\[ {\epsilon }_{t} \sim iid \mr{N}(0,{\sigma }^{2}) \]

Given these assumptions, the log-likelihood function of the transformed data ${Y_{t}}$ is

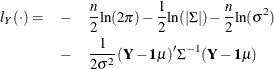
\begin{eqnarray*} l_{Y}({\cdot }) = & -& \frac{n}{2}{\ln }(2{\pi }) - \frac{1}{2}{\ln }(|{\Sigma }|) - \frac{n}{2}{\ln }({\sigma }^{2}) \\ & -& \frac{1}{2{\sigma }^{2}}(\Strong{Y} -\Strong{1} {\mu })’{\Sigma }^{-1}(\Strong{Y} -\Strong{1} {\mu }) \nonumber \end{eqnarray*}

In this equation, n is the number of observations, ${\mu }$ is the mean of $Y_{t}$, 1 is the n-dimensional column vector of 1s, ${{\sigma }^{2}}$ is the innovation variance, ${\mb{Y} =(Y_{1},{\cdots },Y_{n})’}$, and ${{\Sigma }}$ is the covariance matrix of Y.

The log-likelihood function of the original data ${X_{1},{\cdots }, X_{n}}$ is

\[ l_{X}({\cdot }) = l_{Y}({\cdot }) + ({\lambda }-1) \sum _{t=1}^{n}{{\ln }(X_{t}+c)} \]

where c is the value of the CONST= option.

For each value of ${\lambda }$, the maximum log-likelihood of the original data is obtained from the maximum log-likelihood of the transformed data given the maximum likelihood estimate of the autoregressive model.

The maximum log-likelihood values are used to compute the Akaike Information Criterion (AIC) and Schwarz’s Bayesian Criterion (SBC) for each ${\lambda }$ value. The residual mean squared error based on the maximum likelihood estimator is also produced. To compute the mean squared error, the predicted values from the model are transformed again to the original scale (Pankratz 1983, pp. 256–258; Taylor 1986).

After differencing as specified by the DIF= option, the process is assumed to be a stationary autoregressive process. You can check for stationarity of the series with the %DFTEST macro. If the process is not stationary, differencing with the DIF= option is recommended. For a process with moving-average terms, a large value for the AR= option might be appropriate.