Depending on the smoothing model, the smoothing weights consist of the following:
-

-
is a level smoothing weight.
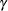
-
is a trend smoothing weight.
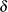
-
is a seasonal smoothing weight.
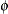
-
is a trend damping weight.
Larger smoothing weights (less damping) permit the more recent data to have a greater influence on the predictions. Smaller smoothing weights (more damping) give less weight to recent data.
Typically the smoothing weights are chosen to be from zero to one. (This is intuitive because the weights associated with the past smoothing state and the value of current observation would normally sum to one.) However, each smoothing model (except Winters Method—Multiplicative Version) has an ARIMA equivalent. Weights chosen to be within the ARIMA additive-invertible region will guarantee stable predictions (Archibald 1990 and Gardner 1985). The ARIMA equivalent and the additive-invertible region for each smoothing model are listed in the following sections.
Smoothing weights are determined so as to minimize the sum of squared, one-step-ahead prediction errors. The optimization is initialized by choosing from a predetermined grid the initial smoothing weights that result in the smallest sum of squared, one-step-ahead prediction errors. The optimization process is highly dependent on this initialization. It is possible that the optimization process will fail due to the inability to obtain stable initial values for the smoothing weights (Greene 1993 and Judge et al. 1980), and it is possible for the optimization to result in a local minima.
The optimization process can result in weights to be chosen outside both the zero-to-one range and the ARIMA additive-invertible region. By restricting weight optimization to additive-invertible region, you can obtain a local minimum with stable predictions. Likewise, weight optimization can be restricted to the zero-to-one range or other ranges. It is also possible to fix certain weights to a specific value and optimize the remaining weights.
The standard errors associated with the smoothing weights are calculated from the Hessian matrix of the sum of squared, one-step-ahead prediction errors with respect to the smoothing weights used in the optimization process.
Sometimes the optimization process results in weights near zero or one.
For simple or double (Brown) exponential smoothing, a level weight near zero implies that simple differencing of the time series might be appropriate.
For linear (Holt) exponential smoothing, a level weight near zero implies that the smoothed trend is constant and that an ARIMA model with deterministic trend might be a more appropriate model.
For damped-trend linear exponential smoothing, a damping weight near one implies that linear (Holt) exponential smoothing might be a more appropriate model.
For Winters method and seasonal exponential smoothing, a seasonal weight near one implies that a nonseasonal model might be more appropriate and a seasonal weight near zero implies that deterministic seasonal factors might be present.