Mixed Logit Model
In mixed logit models, an individual’s utility from any alternative can be decomposed into a deterministic component, ![]() , which is a linear combination of observed variables, and a stochastic component,
, which is a linear combination of observed variables, and a stochastic component, ![]() ,
,
|
|
where ![]() is a vector of observed variables that relate to individual
is a vector of observed variables that relate to individual ![]() and alternative
and alternative ![]() ,
, ![]() is a vector of parameters,
is a vector of parameters, ![]() is an error component that can be correlated among alternatives and heteroscedastic for each individual, and
is an error component that can be correlated among alternatives and heteroscedastic for each individual, and ![]() is a random term with zero mean that is independently and identically distributed over alternatives and individuals. The
conditional logit model is derived if you assume
is a random term with zero mean that is independently and identically distributed over alternatives and individuals. The
conditional logit model is derived if you assume ![]() has an iid Gumbel distribution and
has an iid Gumbel distribution and ![]() .
.
The mixed logit model assumes a general distribution for ![]() and an iid Gumbel distribution for
and an iid Gumbel distribution for ![]() . Denote the density function of the error component
. Denote the density function of the error component ![]() as
as ![]() , where
, where ![]() is a parameter vector of the distribution of
is a parameter vector of the distribution of ![]() . The choice probability of alternative
. The choice probability of alternative ![]() for individual
for individual ![]() is written as
is written as
|
|
where the conditional choice probability for a given value of ![]() is the logit
is the logit
|
|
Since ![]() is not given, the unconditional choice probability,
is not given, the unconditional choice probability, ![]() , is the integral of the conditional choice probability,
, is the integral of the conditional choice probability, ![]() , over the distribution of
, over the distribution of ![]() . This model is called “mixed logit” since the choice probability is a mixture of logits with
. This model is called “mixed logit” since the choice probability is a mixture of logits with ![]() as the mixing distribution.
as the mixing distribution.
In general, the mixed logit model does not have an exact likelihood function because the probability ![]() does not always have a closed form solution. Therefore, a simulation method is used for computing the approximate probability,
does not always have a closed form solution. Therefore, a simulation method is used for computing the approximate probability,
|
|
where ![]() is the number of simulation replications and
is the number of simulation replications and ![]() is a simulated probability. The simulated log-likelihood function is computed as
is a simulated probability. The simulated log-likelihood function is computed as
|
|
where
|
|
For simulation purposes, assume that the error component has a specific structure,
|
|
where ![]() is a vector of observed data and
is a vector of observed data and ![]() is a random vector with zero mean and density function
is a random vector with zero mean and density function ![]() . The observed data vector (
. The observed data vector (![]() ) of the error component can contain some or all elements of
) of the error component can contain some or all elements of ![]() . The component
. The component ![]() induces heteroscedasticity and correlation across unobserved utility components of the alternatives. This allows flexible
substitution patterns among the alternatives. The
induces heteroscedasticity and correlation across unobserved utility components of the alternatives. This allows flexible
substitution patterns among the alternatives. The ![]() th element of vector
th element of vector ![]() is distributed as
is distributed as
|
|
Therefore, ![]() can be specified as
can be specified as
|
|
where
|
|
or
|
|
In addition, ![]() is a vector of random parameters (random coefficients). Random coefficients allow heterogeneity across individuals in their
sensitivity to observed exogenous variables. The observed data vector,
is a vector of random parameters (random coefficients). Random coefficients allow heterogeneity across individuals in their
sensitivity to observed exogenous variables. The observed data vector, ![]() , is a subset of
, is a subset of ![]() . The following three types of distributions for the random coefficients are supported, where the
. The following three types of distributions for the random coefficients are supported, where the ![]() th element of
th element of ![]() is denoted as
is denoted as ![]() :
:
-
Normally distributed coefficient with the mean
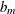 and spread
and spread 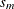 being estimated.
being estimated.
![\[ \beta ^{*}_{m} = b_{m} + s_{m}\epsilon _{\beta } \quad \mbox{and} \quad \epsilon _{\beta } \sim N(0,1) \]](images/etsug_mdc0136.png)
-
Uniformly distributed coefficient with the mean
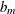 and spread
and spread 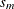 being estimated. A uniform distribution with mean
being estimated. A uniform distribution with mean 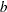 and spread
and spread  is
is 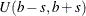 .
.
![\[ \beta ^{*}_{m} = b_{m} + s_{m}\epsilon _{\beta } \quad \mbox{and} \quad \epsilon _{\beta } \sim U(-1, 1) \]](images/etsug_mdc0140.png)
-
Lognormally distributed coefficient. The coefficient is calculated as
![\[ \beta ^{*}_{m} = \exp (b_ m + s_ m \epsilon _{\beta }) \quad \mbox{and} \quad \epsilon _{\beta } \sim N(0,1) \]](images/etsug_mdc0141.png)
where
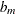 and
and 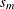 are parameters that are estimated.
are parameters that are estimated.
The estimate of spread for normally, uniformly, and lognormally distributed coefficients can be negative. The absolute value of the estimated spread can be interpreted as an estimate of standard deviation for normally distributed coefficients.
A detailed description of mixed logit models can be found, for example, in Brownstone and Train (1999).