SDATA= Input Data Set

The SDATA= option reads a cross-equation covariance matrix from a data set. The covariance matrix read from the SDATA= data set specified in the SOLVE statement is used to generate random equation errors when the RANDOM= option specifies Monte Carlo simulation.

Typically, the SDATA= data set is created by the OUTS= option in a previous FIT statement. (The OUTS= data set from a FIT statement can be read back in by a SOLVE statement in the same PROC MODEL step.)

You can create an input SDATA= data set by using the DATA step. PROC MODEL expects to find a character variable _NAME_ in the SDATA= data set as well as variables for the equations in the estimation or solution. For each observation with a _NAME_ value that matches the name of an equation, PROC MODEL fills the corresponding row of the 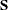matrix with the values of the names of equations found in the data set. If a row or column is omitted from the data set, an identity matrix row or column is assumed. Missing values are ignored. Since the 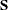matrix is symmetric, you can include only a triangular part of the 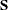matrix in the SDATA= data set with the omitted part indicated by missing values. If the SDATA= data set contains multiple observations with the same _NAME_, the last values supplied for the _NAME_ variable are used. The section OUTS= Data Set contains more details on the format of this data set.

Use the TYPE= option to specify the type of estimation method used to produce the 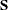matrix you want to input.

ESTDATA= Input Data Set

The ESTDATA= option specifies an input data set that contains an observation with values for some or all of the model parameters. It can also contain observations with the rows of a covariance matrix for the parameters.

When the ESTDATA= option is used, parameter values are set from the first observation. If the RANDOM= option is used and the ESTDATA= data set contains a covariance matrix, the covariance matrix of the parameter estimates is read and used to generate pseudo-random shocks to the model parameters for Monte Carlo simulation. These random perturbations have a multivariate normal distribution with the covariance matrix read from the ESTDATA= data set.

The ESTDATA= data set is usually created by the OUTEST= option in a FIT statement. The OUTEST= data set contains the parameter estimates produced by the FIT statement and also contains the estimated covariance of the parameter estimates if the OUTCOV option is used. This OUTEST= data set can be read in by the ESTDATA= option in a SOLVE statement.

You can also create an ESTDATA= data set with a SAS DATA step program. The data set must contain a numeric variable for each parameter to be given a value or covariance column. The name of the variable in the ESTDATA= data set must match the name of the parameter in the model. Parameters with names longer than 32 characters cannot be set from an ESTDATA= data set. The data set must also contain a character variable _NAME_ of length 32. _NAME_ has a blank value for the observation that gives values to the parameters. _NAME_ contains the name of a parameter for observations that define rows of the covariance matrix.

More than one set of parameter estimates and covariances can be stored in the ESTDATA= data set if the observations for the different estimates are identified by the variable _TYPE_. _TYPE_ must be a character variable of length eight. The TYPE= option is used to select for input the part of the ESTDATA= data set for which the value of the _TYPE_ variable matches the value of the TYPE= option.

OUT= Data Set

The OUT= data set contains solution values, residual values, and actual values of the solution variables.

The OUT= data set contains the following variables:

• BY variables

• RANGE variable

• ID variables

• _TYPE_, a character variable of length eight that identifies the type of observation. The _TYPE_ variable can be PREDICT, RESIDUAL, ACTUAL, or ERROR.

• _MODE_, a character variable of length eight that identifies the solution mode. _MODE_ takes the value FORECAST or SIMULATE.

• if lags are used, a numeric variable, _LAG_, that contains the number of dynamic lags that contribute to the solution. The value of _LAG_ is always zero for STATIC mode solutions. _LAG_ is set to a missing value for lag-starting observations.

• if the RANDOM= option is used, _REP_, a numeric variable that contains the replication number. For example, if RANDOM=10, each input observation results in eleven output observations with _REP_ values 0 through 10. The observations with _REP_=0 are from the unperturbed solution. (The random-number generator functions are suppressed, and the parameter and endogenous perturbations are zero when _REP_=0.)

• _ERRORS_, a numeric variable that contains the number of errors that occurred during the execution of the program for the last iteration for the observation. If the solution failed to converge, this is counted as one error, and the _ERRORS_ variable is made negative.

• solution and other variables. The solution variables contain solution or predicted values for _TYPE_=PREDICT observations, residuals for _TYPE_=RESIDUAL observations, or actual values for _TYPE_=ACTUAL observations. The other model variables, and any other variables read from the input data set, are always actual values from the input data set.

• any other variables named in the OUTVARS statement. These can be program variables computed by the model program, CONTROL variables, parameters, or special variables in the model program. Compound variable names longer than 32 characters are truncated in the OUT= data set.

By default, only the predicted values are written to the OUT= data set. The OUTRESID, OUTACTUAL, and OUTERROR options are used to add the residual, actual, and ERROR. values, respectively, to the data set.

For examples of the OUT= data set, see Example 19.6.

DATA= Input Data Set

The input data set should contain all of the exogenous variables and should supply nonmissing values for them for each period to be solved.

Solution variables can be supplied in the input data set and are used as follows:

• to supply initial lags. For example, if the lag length of the model is three, three observations are read in to feed the lags before any solutions are computed.

• to evaluate the goodness of fit. Goodness-of-fit measures are computed based on the difference between the solved values and the actual values supplied from the data set.

• to supply starting values for the iterative solution. If the value from the input data set for a solution variable is missing, the starting value for it is taken from the solution of the last period (if nonmissing) or else the solution estimate is started at zero.

• for STATIC mode solutions, actual values from the data set are used by the lagging functions for the solution variables.

• for FORECAST mode solutions, actual values from the data set are used as the solution values when nonmissing.