| Testing for Autocorrelation |
The GODFREY= option in the FIT statement produces the Godfrey Lagrange multiplier test for serially correlated residuals for each equation (Godfrey 1978a and 1978b).  is the maximum autoregressive order, and specifies that Godfrey’s tests be computed for lags 1 through
is the maximum autoregressive order, and specifies that Godfrey’s tests be computed for lags 1 through  . The default number of lags is four.
. The default number of lags is four.
The tests are performed separately for each equation estimated by the FIT statement. When a nonlinear model is estimated, the test is computed by using a linearized model.
The following is an example of the output produced by the GODFREY=3 option:
| Godfrey Test Output |
| Godfrey's Serial Correlation Test | |||
|---|---|---|---|
| Equation | Alternative | LM | Pr > LM |
| y | 1 | 6.63 | 0.0100 |
| 2 | 6.89 | 0.0319 | |
| 3 | 6.96 | 0.0732 | |
The three variations of the test reported by the GODFREY=3 option are designed to have power against different alternative hypothesis. Thus, if the residuals in fact have only first-order autocorrelation, the lag 1 test has the most power for rejecting the null hypothesis of uncorrelated residuals. If the residuals have second- but not higher-order autocorrelation, the lag 2 test might be more likely to reject; the same is true for third-order autocorrelation and the lag 3 test.
The null hypothesis of Godfrey’s tests is that the equation residuals are white noise. However, if the equation includes autoregressive error model of order 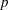 (AR(
(AR(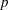 ),) then the lag
),) then the lag 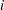 test, when considered in terms of the structural error, is for the null hypothesis that the structural errors are from an AR(
test, when considered in terms of the structural error, is for the null hypothesis that the structural errors are from an AR(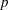 ) process versus the alternative hypothesis that the errors are from an AR(
) process versus the alternative hypothesis that the errors are from an AR(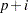 ) process.
) process.
The alternative ARMA(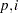 ) process is locally equivalent to the alternative AR(
) process is locally equivalent to the alternative AR(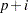 ) process with respect to the null model AR(
) process with respect to the null model AR(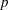 ). Thus, the GODFREY= option results are also a test of AR(
). Thus, the GODFREY= option results are also a test of AR(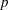 ) errors against the alternative hypothesis of ARMA(
) errors against the alternative hypothesis of ARMA(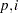 ) errors. See Godfrey (1978a and 1978b) for more detailed information.
) errors. See Godfrey (1978a and 1978b) for more detailed information.