| The SYSLIN Procedure |
| ANOVA Table for Instrumental Variables Methods |
In the instrumental variables methods (2SLS, LIML, K-class, MELO), first-stage predicted values are substituted for the endogenous regressors. As a result, the regression sum of squares (RSS) and the error sum of squares (ESS) do not sum to the total corrected sum of squares for the dependent variable (TSS). The analysis-of-variance table included in the second-stage results gives these sums of squares and the mean squares that are used for the 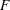 test, but this table is not a variance decomposition in the usual sense.
test, but this table is not a variance decomposition in the usual sense.
The 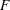 test shown in the instrumental variables case is a valid test of the no-regression hypothesis that the true coefficients of all regressors are 0. However, because of the first-stage projection of the regression mean square, this is a Wald-type test statistic, which is asymptotically
test shown in the instrumental variables case is a valid test of the no-regression hypothesis that the true coefficients of all regressors are 0. However, because of the first-stage projection of the regression mean square, this is a Wald-type test statistic, which is asymptotically 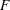 but not exactly
but not exactly 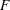 -distributed in finite samples. Thus, for small samples the
-distributed in finite samples. Thus, for small samples the 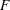 test is only approximate when instrumental variables are used.
test is only approximate when instrumental variables are used.
Copyright © SAS Institute, Inc. All Rights Reserved.