In simultaneous systems of equations, endogenous variables are determined jointly rather than sequentially. Consider the following supply and demand functions for some product:

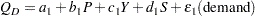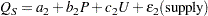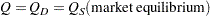The variables in this system are as follows:

Q

quantity demanded

Q

quantity supplied

Q

the observed quantity sold, which equates quantity supplied and quantity demanded in equilibrium

P

price per unit

Y

income

S

price of substitutes

U

unit cost

the random error term for the demand equation

the random error term for the supply equation

In this system, quantity demanded depends on price, income, and the price of substitutes. Consumers normally purchase more of a product when prices are lower and when income and the price of substitute goods are higher. Quantity supplied depends on price and the unit cost of production. Producers supply more when price is high and when unit cost is low. The actual price and quantity sold are determined jointly by the values that equate demand and supply.

Since price and quantity are jointly endogenous variables, both structural equations are necessary to adequately describe the observed values. A critical assumption of OLS is that the regressors are uncorrelated with the residual. When current endogenous variables appear as regressors in other equations (endogenous variables depend on each other), this assumption is violated and the OLS parameter estimates are biased and inconsistent. The bias caused by the violated assumptions is called simultaneous equation bias. Neither the demand nor supply equation can be estimated consistently by OLS.