PROC PDLREG: MODEL Statement :: SAS/ETS(R) 9.22 User's Guide

The PDLREG Procedure

MODEL Statement

MODEL dependent = effects / options ;

The MODEL statement specifies the regression model. The keyword MODEL is followed by the dependent variable name, an equal sign, and a list of independent effects. Only one MODEL statement is allowed.

Every variable in the model must be a numeric variable in the input data set. Specify an independent effect with a variable name optionally followed by a polynomial lag distribution specification.

Specifying Independent Effects

The general form of an effect is

variable ( length, degree, minimum-degree, constraint )

The term in parentheses following the variable name specifies a polynomial distributed lag (PDL) for the variable. The PDL specification is as follows:

length: specifies the number of lags of the variable to include in the lag distribution.
degree: specifies the maximum degree of the distribution polynomial. If not specified, the degree defaults to the lag length.
minimum-degree: specifies the minimum degree of the polynomial. By default minimum-degree is the same as degree.
constraint: specifies endpoint restrictions on the polynomial. The value of constraint can be FIRST, LAST, or BOTH. If a value is not specified, there are no endpoint restrictions.

If you do not specify the degree or minimum-degree parameter, but you do specify endpoint restrictions, you must use commas to show which parameter, degree or minimum-degree, is left out.

MODEL Statement Options

The following options can appear in the MODEL statement after a slash (/).

ALL

prints all the matrices computed during the analysis of the model.

COEF

prints the transformation coefficients for the first p observations. These coefficients are formed from a scalar multiplied by the inverse of the Cholesky root of the Toeplitz matrix of autocovariances.

CORRB

prints the matrix of estimated correlations between the parameter estimates.

COVB

prints the matrix of estimated covariances between the parameter estimates.

DW= j

prints the generalized Durbin-Watson statistics up to the order of j. The default is DW=1. When you specify the LAGDEP or LAGDEP=name option, the Durbin-Watson statistic is not printed unless you specify the DW= option.

DWPROB

prints the marginal probability of the Durbin-Watson statistic.

CONVERGE= value

sets the convergence criterion. If the maximum absolute value of the change in the autoregressive parameter estimates between iterations is less than this amount, then convergence is assumed. The default is CONVERGE=.001.

GINV

prints the inverse of the Toeplitz matrix of autocovariances for the Yule-Walker solution.

I

prints 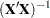$\text{[math]}$ , the inverse of the crossproducts matrix for the model; or, if restrictions are specified, it prints 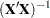$\text{[math]}$ adjusted for the restrictions.

ITPRINT

prints information on each iteration.

LAGDEP

LAGDV

prints the t statistic for testing residual autocorrelation when regressors contain lagged dependent variables.

LAGDEP= name

LAGDV= name

prints the Durbin h statistic for testing the presence of first-order autocorrelation when regressors contain the lagged dependent variable whose name is specified as LAGDEP=name. When the h statistic cannot be computed, the asymptotically equivalent t statistic is given.

MAXITER= number

sets the maximum number of iterations allowed. The default is MAXITER=50.

METHOD= value

specifies the type of estimates for the autoregressive component. The values of the METHOD= option are as follows:

METHOD=ML: specifies the maximum likelihood method.
METHOD=ULS: specifies unconditional least squares.
METHOD=YW: specifies the Yule-Walker method.
METHOD=ITYW: specifies iterative Yule-Walker estimates.

The default is METHOD=ML if you specified the LAGDEP or LAGDEP= option; otherwise, METHOD=YW is the default.

NLAG= m

NLAG= ( number-list )

specifies the order of the autoregressive process or the subset of autoregressive lags to be fit. If you do not specify the NLAG= option, PROC PDLREG does not fit an autoregressive model.

NOINT

suppresses the intercept parameter from the model.

NOPRINT

suppresses the printed output.

PARTIAL

prints partial autocorrelations if the NLAG= option is specified.

STB

prints standardized parameter estimates. Sometimes known as a standard partial regression coefficient, a standardized parameter estimate is a parameter estimate multiplied by the standard deviation of the associated regressor and divided by the standard deviation of the regressed variable.

XPX

prints the crossproducts matrix, 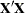$\text{[math]}$ , used for the model. X refers to the transformed matrix of regressors for the regression.

Top of Page