| The PANEL Procedure |
| R-Square |
The conventional R-square measure is inappropriate for all models that the PANEL procedure estimates by using GLS since a number outside the [0,1] range might be produced. Hence, a generalization of the R-square measure is reported. The following goodness-of-fit measure (Buse 1973) is reported:
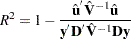 |
where  are the residuals of the transformed model,
are the residuals of the transformed model, 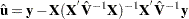 ,
,
and 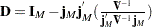 .
.
This is a measure of the proportion of the transformed sum of squares of the dependent variable that is attributable to the influence of the independent variables.
If there is no intercept in the model, the corresponding measure (Theil 1961) is
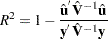 |
However, the fixed-effects models are somewhat different. In the case of a fixed-effects model, the choice of including or excluding an intercept becomes merely a choice of classification. Suppressing the intercept in the FIXONE or FIXONETIME case merely changes the name of the intercept to a fixed effect. It makes no sense to redefine the R-square measure since nothing material changes in the model. Similarly, for the FIXTWO model there is no reason to change R-square. In the case of the FIXONE, FIXONETIME, and FIXTWO models, the R-square is defined as the Theil (1961) R-square (detailed above). This makes intuitive sense since you are regressing a transformed (demeaned) series on transformed regressors, excluding a constant. In other words, you are looking at one minus the sum of squared errors divided by the sum of squares of the (transformed) dependent variable.
In the case of OLS estimation, both of the R-square formulas given here reduce to the usual R-square formula.
Copyright © SAS Institute, Inc. All Rights Reserved.