| The PANEL Procedure |
| Restricted Estimates |
A consequence of estimating a linear model with a restriction is that the error degrees of freedom increase by the number of restrictions. PROC PANEL produces the Lagrange multiplier associated with each restriction.
Say that you are interested in linear regression in which there are  restrictions. A linear restriction implies the following set of equations that relate the regression coefficients:
restrictions. A linear restriction implies the following set of equations that relate the regression coefficients:
 |
To economize on notation, you can represent the restriction structure in the following matrix notation 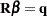 . The restricted
. The restricted 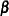 estimator is given by:
estimator is given by:
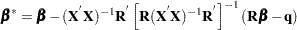 |
The Lagrange multipliers are given as:
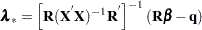 |
The standard errors of the Lagrange Multipliers are calculated from the following relationship:
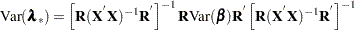 |
A significant Lagrange multiplier implies that you can reject the null hypothesis that the restrictions are not binding.
Note that in the special case of the fixed-effects models, the NOINT option and RESTRICT INTERCEPT=0 option give different estimates. This is not an error; it reflects two perspectives on the same issue. In the FIXONE case, the intercept is the last cross section’s fixed effect (or the last time affecting the case of FIXONETIME). Specifying the NOINT option removes the intercept, but allows the last effect in. The NOINT command simply reclassifies the effects. The dummy variables become true cross section effects. If you specify the NOINT option with the FIXTWO option, the restriction is imposed that the last time effect is zero. A RESTRICT INTERCEPT=0 statement suppresses the estimation of the last effect in the FIXONE and FIXONETIME case. A RESTRICT INTERCEPT=0 has similar effects on the FIXTWO estimator. In general, restricting the intercept to zero is not recommended because OLS loses its unbiased nature.
Copyright © SAS Institute, Inc. All Rights Reserved.