The VARMAX procedure enables you to model the dynamic relationship both between the dependent variables and between the dependent and independent variables. The VARMAX procedure includes the following features:

• several modeling features:

  • vector autoregressive model

  • vector autoregressive model with exogenous variables

  • vector autoregressive and moving-average model

  • Bayesian vector autoregressive model

  • vector error correction model

  • Bayesian vector error correction model

  • GARCH-type multivariate conditional heteroscedasticity models

• criteria for automatically determining AR and MA orders:

  • Akaike information criterion (AIC)

  • corrected AIC (AICC)

  • Hannan-Quinn (HQ) criterion

  • final prediction error (FPE)

  • Schwarz Bayesian criterion (SBC), also known as Bayesian information criterion (BIC)

• AR order identification aids:

  • partial cross-correlations

  • Yule-Walker estimates

  • partial autoregressive coefficients

  • partial canonical correlations

• testing the presence of unit roots and cointegration:

  • Dickey-Fuller tests

  • Johansen cointegration test for nonstationary vector processes of integrated order one

  • Stock-Watson common trends test for the possibility of cointegration among nonstationary vector processes of integrated order one

  • Johansen cointegration test for nonstationary vector processes of integrated order two

• model parameter estimation methods:

  • least squares (LS)

  • maximum likelihood (ML)

• model checks and residual analysis using the following tests:

  • Durbin-Watson (DW) statistics

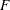  • test for autoregressive conditional heteroscedastic (ARCH) disturbance

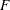  • test for AR disturbance

  • Jarque-Bera normality test

  • Portmanteau test

• seasonal deterministic terms

• subset models

• multiple regression with distributed lags

• dead-start model that does not have present values of the exogenous variables

• Granger-causal relationships between two distinct groups of variables

• infinite order AR representation

• impulse response function (or infinite order MA representation)

• decomposition of the predicted error covariances

• roots of the characteristic functions for both the AR and MA parts to evaluate the proximity of the roots to the unit circle

• contemporaneous relationships among the components of the vector time series

• forecasts

• conditional covariances for GARCH models