| The ARIMA Procedure |
| Initial Values |
The syntax for giving initial values to transfer function parameters in the INITVAL= option parallels the syntax of the INPUT= option. For each transfer function in the INPUT= option, the INITVAL= option should give an initialization specification followed by the input series name. The initialization specification for each transfer function has the form
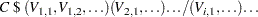 |
where C is the lag 0 term in the first numerator factor of the transfer function (or the overall scale factor if the ALTPARM option is specified) and 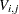 is the coefficient of the
is the coefficient of the 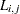 element in the transfer function.
element in the transfer function.
To illustrate, suppose you want to fit the model
 |
and start the estimation process with the initial values  =10,
=10, 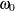 =1,
=1,  =0.5,
=0.5, 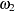 =0.03,
=0.03,  =0.8,
=0.8, 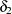 =–0.1,
=–0.1, 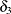 =0.002,
=0.002, 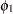 =0.1,
=0.1, 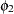 =0.01. (These are arbitrary values for illustration only.) You would use the following statements:
=0.01. (These are arbitrary values for illustration only.) You would use the following statements:
identify var=y crosscorr=x;
estimate p=(1,3) input=(3$(1,2)/(1,2,3)x)
mu=10 ar=.1 .01
initval=(1$(.5,.03)/(.8,-.1,.002)x);
Note that the lags specified for a particular factor are sorted, so initial values should be given in sorted order. For example, if the P= option had been entered as P=(3,1) instead of P=(1,3), the model would be the same and so would the AR= option. Sorting is done within all factors, including transfer function factors, so initial values should always be given in order of increasing lags.
Here is another illustration, showing initialization for a factored model with multiple inputs. The model is
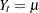 |
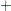 |
 |
|||
 |
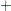 |
 |
and the initial values are  =10,
=10, 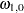 =5,
=5, 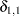 =0.8,
=0.8, 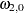 =1,
=1, 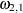 =0.5,
=0.5, 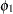 =0.1,
=0.1,  =0.05, and
=0.05, and 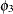 =0.01. You would use the following statements:
=0.01. You would use the following statements:
identify var=y crosscorr=(w x);
estimate p=(1)(6,12) input=(/(1)w, 3$(1)x)
mu=10 ar=.1 .05 .01
initval=(5$/(.8)w 1$(.5)x);
Copyright © SAS Institute, Inc. All Rights Reserved.