ARIMA options ;

The ARIMA statement applies the X-11-ARIMA method to the series specified in the VAR statement. This method uses an ARIMA model estimated from the original data to extend the series one or more years. The ARIMA statement options control the ARIMA model used and the estimation, forecasting, and printing of this model.

There are two ways of obtaining an ARIMA model to extend the series. A model can be given explicitly with the MODEL= and TRANSFORM= options. Alternatively, the best-fitting model from a set of five predefined models is found automatically whenever the MODEL= option is absent. See the section Details of Model Selection for details.

BACKCAST= n

specifies the number of years to backcast the series. The default is BACKCAST= 0. See the section Effect of Backcast and Forecast Length for details.

CHICR= value

specifies the criteria for the significance level for the Box-Ljung chi-square test for lack of fit when testing the five predefined models. The default is CHICR= 0.05. The CHICR= option values must be between 0.01 and 0.90. The hypothesis being tested is that of model adequacy. Nonrejection of the hypothesis is evidence for an adequate model. Making the CHICR= value smaller makes it easier to accept the model. See the section Criteria Details for further details on the CHICR= option.

CONVERGE= value

specifies the convergence criterion for the estimation of an ARIMA model. The default value is 0.001. The CONVERGE= value must be positive.

FORECAST= n

specifies the number of years to forecast the series. The default is FORECAST= 1. See the section Effect of Backcast and Forecast Length for details.

MAPECR= value

specifies the criteria for the mean absolute percent error (MAPE) when testing the five predefined models. A small MAPE value is evidence for an adequate model; a large MAPE value results in the model being rejected. The MAPECR= value is the boundary for acceptance/rejection. Thus a larger MAPECR= value would make it easier for a model to pass the criteria. The default is MAPECR= 15. The MAPECR= option values must be between 1 and 100. See the section Criteria Details for further details on the MAPECR= option.

MAXITER= n

specifies the maximum number of iterations in the estimation process. MAXITER must be between 1 and 60; the default value is 15.

METHOD= CLS

METHOD= ULS

METHOD= ML

specifies the estimation method. ML requests maximum likelihood, ULS requests unconditional least squares, and CLS requests conditional least squares. METHOD=CLS is the default. The maximum likelihood estimates are more expensive to compute than the conditional least squares estimates. In some cases, however, they can be preferable. For further information on the estimation methods, see Estimation Details in Chapter 7, The ARIMA Procedure.

MODEL= ( P=n1 Q=n2 SP=n3 SQ=n4 DIF=n5 SDIF=n6 <NOINT> <CENTER>)

specifies the ARIMA model. The AR and MA orders are given by P=n1 and Q=n2, respectively, while the seasonal AR and MA orders are given by SP=n3 and SQ=n4, respectively. The lag corresponding to seasonality is determined by the MONTHLY or QUARTERLY statement. Similarly, differencing and seasonal differencing are given by DIF=n5 and SDIF=n6, respectively.

For example

   arima model=( p=2 q=1 sp=1 dif=1 sdif=1 );

specifies a (2,1,1)(1,1,0)s model, where s, the seasonality, is either 12 (monthly) or 4 (quarterly). More examples of the MODEL= syntax are given in the section Details of Model Selection.

NOINT

suppresses the fitting of a constant (or intercept) parameter in the model. (That is, the parameter 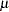is omitted.)

CENTER

centers each time series by subtracting its sample mean. The analysis is done on the centered data. Later, when forecasts are generated, the mean is added back. Note that centering is done after differencing. The CENTER option is normally used in conjunction with the NOCONSTANT option of the ESTIMATE statement.

For example, to fit an AR(1) model on the centered data without an intercept, use the following ARIMA statement:

   arima model=( p=1 center noint );

NOPRINT

suppresses the normal printout generated by the ARIMA statement. Note that the effect of specifying the NOPRINT option in the ARIMA statement is different from the effect of specifying the NOPRINT in the PROC X11 statement, since the former only affects ARIMA output.

OVDIFCR= value

specifies the criteria for the over-differencing test when testing the five predefined models. When the MA parameters in one of these models sum to a number close to 1.0, this is an indication of over-parameterization and the model is rejected. The OVDIFCR= value is the boundary for this rejection; values greater than this value fail the over-differencing test. A larger OVDIFCR= value would make it easier for a model to pass the criteria. The default is OVDIFCR= 0.90. The OVDIFCR= option values must be between 0.80 and 0.99. See the section Criteria Details for further details on the OVDIFCR= option.

PRINTALL

provides the same output as the default printing for all models fit and, in addition, prints an estimation summary and chi-square statistics for each model fit. See Printed Output for details.

PRINTFP

prints the results for the initial pass of X11 made to exclude trading-day effects. This option has an effect only when the TDREGR= option specifies ADJUST, TEST, or PRINT. In these cases, an initial pass of the standard X11 method is required to get rid of calendar effects before doing any ARIMA estimation. Usually this first pass is not of interest, and by default no tables are printed. However, specifying PRINTFP in the ARIMA statement causes any tables printed in the final pass to also be printed for this initial pass.

TRANSFORM= (LOG) | LOG

TRANSFORM= ( constant ** power )

The ARIMA statement in PROC X11 allows certain transformations on the series before estimation. The specified transformation is applied only to a user-specified model. If TRANSFORM= is specified and the MODEL= option is not specified, the transformation request is ignored and a warning is printed.

The LOG transformation requests that the natural log of the series be used for estimation. The resulting forecast values are transformed back to the original scale.

A general power transformation of the form 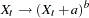is obtained by specifying

   transform= ( a ** b )

If the constant a is not specified, it is assumed to be zero. The specified ARIMA model is then estimated using the transformed series. The resulting forecast values are transformed back to the original scale.