Multivariate GARCH Models—New GARCH Statement

Multivariate GARCH modeling is now a production feature of VARMAX.

To enable greater flexibility in specifying multivariate GARCH models, the new GARCH statement has been added to the VARMAX procedure. With the addition of the GARCH statement, the GARCH= option is no longer supported on the MODEL statement.

The OUTHT= option can be specified in the GARCH statement to write the estimated conditional covariance matrix to an output data set. See GARCH Statement in Chapter 30, The VARMAX Procedure, for details.

The VARMAX Model

The VARMAX procedure provides modeling of a VARMAX(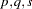) process which is written as

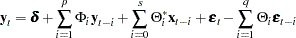where , , 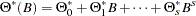and .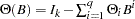

If the Kalman filtering method is used for the parameter estimation of the VARMAX(,,) model, then the dimension of the state-space vector is large, which takes time and memory for computing. For convenience, the parameter estimation of the VARMAX(,,) model uses the two-stage estimation method, which computes the estimation of deterministic terms and exogenous parameters and then maximizes the log-likelihood function of the VARMA(,) model.

Some examples of VARMAX modeling are:

   model y1 y2 = x1 / q=1;
   nloptions tech=qn;

   model y1 y2 = x1 / p=1 q=1 xlag=1 nocurrentx;
   nloptions tech=qn;

The BVARX Model

Bayesian modeling allows independent (exogenous) variables with their distributed lags. For example:

   model y1 y2 = x1 / p=2 prior=(theta=0.2 lambda=5);

The VECMX Model

Vector error correction modeling now allows independent (exogenous) variables with their distributed lags. For example:

   model y1 y2 = x1 / p=2 ecm=(rank=1);

The BVECMX Model

Bayesian vector error correction modeling allows independent (exogenous) variables with their distributed lags. For example:

   model y1 y2 = x1 / p=2 prior=(theta=0.2 lambda=5)  ecm=(rank=1);

The VARMAX-GARCH Model

VARMAX modeling now supports an error term that has a GARCH-type multivariate conditional heteroscedasticity model. For example:

   model y1 y2 = x1 / p=1 q=1;
   garch q=1;

New Printing Control Options

The PRINT= option can be used in the MODEL statement to control the results printed. See the description of the PRINT= option in Chapter 30, The VARMAX Procedure, for details.