| The VARMAX Procedure |
| COINTEG Statement |
- COINTEG RANK=number < H=(matrix) > < J=(matrix) >
< EXOGENEITY > < NORMALIZE=variable > ;
The COINTEG statement fits the vector error correction model to the data, tests the restrictions of the long-run parameters and the adjustment parameters, and tests for the weak exogeneity in the long-run parameters. The cointegrated system uses the maximum likelihood analysis proposed by Johansen and Juselius (1990) and Johansen (1995a, 1995b). Only one COINTEG statement is allowed.
You specify the ECM= option in the MODEL statement or the COINTEG statement to fit the VECM( ). The P= option in the MODEL statement is used to specify the autoregressive order of the VECM.
). The P= option in the MODEL statement is used to specify the autoregressive order of the VECM.
The following statements are equivalent for fitting a VECM(2).
proc varmax data=one;
model y1-y3 / p=2 ecm=(rank=1);
run;
proc varmax data=one;
model y1-y3 / p=2;
cointeg rank=1;
run;
To test restrictions of either  or
or 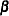 or both, you specify either J= or H= or both, respectively. You specify the EXOGENEITY option in the COINTEG statement for tests of the weak exogeneity in the long-run parameters.
or both, you specify either J= or H= or both, respectively. You specify the EXOGENEITY option in the COINTEG statement for tests of the weak exogeneity in the long-run parameters.
The following is an example of the COINTEG statement.
proc varmax data=one;
model y1-y3 / p=2;
cointeg rank=1 h=(1 0, -1 0, 0 1)
j=(1 0, 0 0, 0 1) exogeneity;
run;
The following options can be used in the COINTEG statement:
- EXOGENEITY
formulates the likelihood ratio tests for testing weak exogeneity in the long-run parameters. The null hypothesis is that one variable is weakly exogenous for the others.
- H=(matrix)
specifies the restrictions
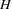 on the
on the 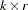 or
or 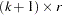 cointegrated coefficient matrix
cointegrated coefficient matrix 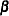 such that
such that 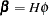 , where
, where 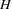 is known and
is known and 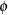 is unknown. If the VECM(
is unknown. If the VECM( ) is specified with the COINTEG statement or with the ECM= option in the MODEL statement and the ECTREND option is not included with the ECM= specification, then the
) is specified with the COINTEG statement or with the ECM= option in the MODEL statement and the ECTREND option is not included with the ECM= specification, then the 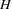 matrix has dimension
matrix has dimension 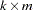 . If the VECM(
. If the VECM( ) is specified with the COINTEG statement or with the ECM= option in the MODEL statement and the ECTREND option is also used, then the
) is specified with the COINTEG statement or with the ECM= option in the MODEL statement and the ECTREND option is also used, then the 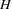 matrix has dimension
matrix has dimension 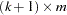 . Here
. Here 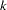 is the number of dependent variables, and
is the number of dependent variables, and 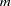 is
is 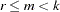 where
where  is defined with the RANK=
is defined with the RANK= option.
option. For example, consider a system that contains four variables and the RANK=1 option with
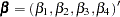 . The restriction matrix for the test of
. The restriction matrix for the test of 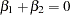 can be specified as
can be specified as cointeg rank=1 h=(1 0 0, -1 0 0, 0 1 0, 0 0 1);
Here the matrix H is
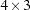 where
where 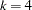 and
and 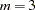 , and each row of the matrix H is separated by commas.
, and each row of the matrix H is separated by commas. When the series has no separate deterministic trend, the constant term should be restricted by
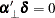 . In the preceding example, the
. In the preceding example, the 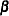 can be either
can be either 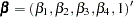 or
or 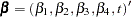 . You can specify the restriction matrix for the previous test of
. You can specify the restriction matrix for the previous test of 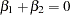 as follows:
as follows: cointeg rank=1 h=(1 0 0 0, -1 0 0 0, 0 1 0 0, 0 0 1 0, 0 0 0 1);When the cointegrated system contains three dependent variables and the RANK=2 option, you can specify the restriction matrix for the test of
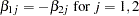 as follows:
as follows: cointeg rank=2 h=(1 0, -1 0, 0 1);
- J=(matrix)
specifies the restrictions
 on the
on the 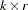 adjustment matrix
adjustment matrix  such that
such that 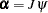 , where
, where  is known and
is known and 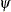 is unknown. The
is unknown. The 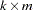 matrix
matrix  is specified by using this option, where
is specified by using this option, where 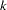 is the number of dependent variables,
is the number of dependent variables, 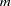 is
is 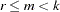 , and
, and  is defined with the RANK=
is defined with the RANK= option.
option. For example, when the system contains four variables and the RANK=1 option is used, you can specify the restriction matrix for the test of
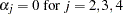 as follows:
as follows: cointeg rank=1 j=(1, 0, 0, 0);
When the system contains three variables and the RANK=2 option, you can specify the restriction matrix for the test of
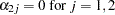 as follows:
as follows: cointeg rank=2 j=(1 0, 0 0, 0 1);
- NORMALIZE=variable
specifies a single dependent (endogenous) variable name whose cointegrating vectors are normalized. If the variable name is different from that specified in the COINTTEST=(JOHANSEN= ) or ECM= option in the MODEL statement, the variable name specified in the COINTEG statement is used. If the normalized variable is not specified, cointegrating vectors are not normalized.
- RANK=number
specifies the cointegration rank of the cointegrated system. This option is required in the COINTEG statement. The rank of cointegration should be greater than zero and less than the number of dependent (endogenous) variables. If the value of the RANK= option in the COINTEG statement is different from that specified in the ECM= option, the rank specified in the COINTEG statement is used.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.