MODEL response = regressors / options ;

The MODEL statement specifies the regression model and the error structure assumed for the regression residuals. The response variable on the left side of the equal sign is regressed on the independent variables listed after the equal sign. Any number of MODEL statements can be used. For each model statement, only one response variable can be specified on the left side of the equal sign.

The error structure is specified by the FIXONE, FIXTWO, RANONE, RANTWO, FULLER, PARKS, and DASILVA options. More than one of these options can be used, in which case the analysis is repeated for each error structure model specified.

Models can be given labels up to 32 characters in length. Model labels are used in the printed output to identify the results for different models. If no label is specified, the response variable name is used as the label for the model. The model label is specified as follows:

label:

MODEL response = regressors / options ;

The following options can be specified on the MODEL statement after a slash (/).

CORRB

CORR

prints the matrix of estimated correlations between the parameter estimates.

COVB

VAR

prints the matrix of estimated covariances between the parameter estimates.

FIXONE

specifies that a one-way fixed-effects model be estimated with the one-way model that corresponds to group effects only.

FIXTWO

specifies that a two-way fixed-effects model be estimated.

RANONE

specifies that a one-way random-effects model be estimated.

RANTWO

specifies that a two-way random-effects model be estimated.

FULLER

specifies that the model be estimated by using the Fuller-Battese method, which assumes a variance components model for the error structure.

PARKS

specifies that the model be estimated by using the Parks method, which assumes a first-order autoregressive model for the error structure.

DASILVA

specifies that the model be estimated by using the Da Silva method, which assumes a mixed variance-component moving-average model for the error structure.

M=number

specifies the order of the moving-average process in the Da Silva method. The M= value must be less than . The default is M=1.

PHI

prints the 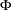matrix of estimated covariances of the observations for the Parks method. The PHI option is relevant only when the PARKS option is used.

RHO

prints the estimated autocorrelation coefficients for the Parks method.

NOINT

NOMEAN

suppresses the intercept parameter from the model.

NOPRINT

suppresses the normal printed output.

SINGULAR=number

specifies a singularity criterion for the inversion of the matrix. The default depends on the precision of the computer system.