specifies an output SAS data set for residuals and predicted values. The OUT= option is used in conjunction with the OUTPUT statement. See the section OUT= Data Set for details.

writes the parameter estimates to an output data set. See the section OUTEST= Data Set for details.

writes the covariance matrix of the parameter estimates to the OUTEST= data set in addition to the parameter estimates.

writes covariance matrices for each model in a system to the OUTEST= data set when the 3SLS, SUR, or FIML option is used.

writes the sum-of-squares-and-crossproducts matrix to an output data set. See the section OUTSSCP= Data Set for details.

specifies the three-stage least squares estimation method.

specifies Fuller’s modification to the LIML estimation method. See the section Fuller’s Modification to LIML for details.

specifies the convergence criterion for the iterative estimation methods IT3SLS, ITSUR, and FIML. The default is CONVERGE=0.0001.

specifies the full information maximum likelihood estimation method.

specifies the iterative seemingly unrelated estimation method.

specifies the iterative three-stage least squares estimation method.

specifies the K-class estimation method.

specifies the limited information maximum likelihood estimation method.

specifies the maximum number of iterations allowed for the IT3SLS, ITSUR, and FIML estimation methods. The MAXITER= option can be abbreviated as MAXIT=. The default is MAXITER=30.

specifies the minimum expected loss estimation method.

excludes the RESTRICT statements from the final stage for the 3SLS, IT3SLS, SUR, and ITSUR estimation methods.

specifies the ordinary least squares estimation method. This is the default.

uses the diagonal of S instead of S to do the estimation, where S is the covariance matrix of equation errors. See the section Uncorrelated Errors across Equations for details.

specifies a criterion for testing singularity of the crossproducts matrix. This is a tuning parameter used to make PROC SYSLIN more or less sensitive to singularities. The value must be between 0 and 1. The default is SINGULAR=1E–8.

specifies the seemingly unrelated estimation method.

prints first-stage regression statistics for the endogenous variables regressed on the instruments. This output includes sums of squares, estimates, variances, and standard deviations.

prints parameter estimates, system-weighted residual sum of squares, and 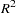at each iteration for the IT3SLS and ITSUR estimation methods. For the FIML method, the ITPRINT option prints parameter estimates, negative of log-likelihood function, and norm of gradient vector at each iteration.

suppresses all printed output. Specifying NOPRINT in the PROC SYSLIN statement is equivalent to specifying NOPRINT in every MODEL statement.

prints the reduced form estimates. If the REDUCED option is specified, you should specify any IDENTITY statements needed to make the system square. See the section Reduced Form Estimates for details.

prints descriptive statistics for the dependent variables. The statistics printed include the sum, mean, uncorrected sum of squares, variance, and standard deviation.

prints the uncorrected sum-of-squares-and-crossproducts matrix.

prints the uncorrected sum-of-squares-and-crossproducts matrix for all variables used in the analysis, including predicted values of variables generated by the procedure.

specifies the denominator to use in calculating cross-equation error covariances and parameter standard errors and covariances. The default is VARDEF=DF, which corrects for model degrees of freedom. VARDEF=N specifies no degrees-of-freedom correction. VARDEF=WEIGHT specifies the sum of the observation weights. VARDEF=WGT specifies the sum of the observation weights minus the model degrees of freedom. See the section Computation of Standard Errors for details.