PROC SPECTRA prints two test statistics for white noise when the WHITETEST option is specified: Fisher’s Kappa (Davis 1941, Fuller 1976) and Bartlett’s Kolmogorov-Smirnov statistic (Bartlett 1966, Fuller 1976, Durbin 1967).

If the time series is a sequence of independent random variables with mean 0 and variance 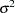, then the periodogram, 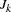, will have the same expected value for all 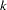. For a time series with nonzero autocorrelation, each ordinate of the periodogram, 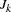, will have different expected values. The Fisher’s Kappa statistic tests whether the largest 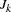can be considered different from the mean of the 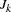. Critical values for the Fisher’s Kappa test can be found in Fuller 1976.

The Kolmogorov-Smirnov statistic reported by PROC SPECTRA has the same asymptotic distribution as Bartlett’s test (Durbin 1967). The Kolmogorov-Smirnov statistic compares the normalized cumulative periodogram with the cumulative distribution function of a uniform(0,1) random variable. The normalized cumulative periodogram, 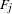, of the series is

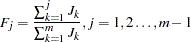where 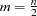if is even or 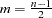if is odd. The test statistic is the maximum absolute difference of the normalized cumulative periodogram and the uniform cumulative distribution function. Approximate p-values for Bartlett’s Kolmogorov-Smirnov test statistics are provided with the test statistics. Small p-values cause you to reject the null-hypothesis that the series is white noise.