| The QLIM Procedure |
| Stochastic Frontier Production and Cost Models |
Stochastic frontier production models were first developed by Aigner, Lovell, and Schmidt (1977) and Meeusen and van den Broeck (1977). Specification of these models allow for random shocks of the production or cost but also include a term for technological or cost inefficiency. Assuming that the production function takes a log-linear Cobb-Douglas form, the stochastic frontier production model can be written as
 |
where 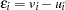 . The
. The  term represents the stochastic error component and
term represents the stochastic error component and 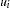 is the nonnegative, technology inefficiency error component. The
is the nonnegative, technology inefficiency error component. The  error component is assumed to be distributed iid normal and independently from
error component is assumed to be distributed iid normal and independently from 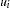 . If
. If  , the error term,
, the error term, 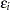 , is negatively skewed and represents technology inefficiency. If
, is negatively skewed and represents technology inefficiency. If 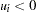 , the error term
, the error term 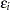 is positively skewed and represents cost inefficiency. PROC QLIM models the
is positively skewed and represents cost inefficiency. PROC QLIM models the 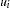 error component as a half normal, exponential, or truncated normal distribution.
error component as a half normal, exponential, or truncated normal distribution.
The Normal-Half Normal Model
In case of the normal-half normal model,  is iid
is iid  ,
, 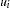 is iid
is iid  with
with  and
and 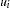 independent of each other. Given the independence of error terms, the joint density of
independent of each other. Given the independence of error terms, the joint density of  and
and  can be written as
can be written as
 |
Substituting  into the preceding equation gives
into the preceding equation gives
 |
Integrating  out to obtain the marginal density function of
out to obtain the marginal density function of  results in the following form:
results in the following form:
 |
 |
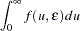 |
|||
 |
 |
 |
|||
 |
 |
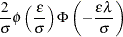 |
where  and
and  .
.
In the case of a stochastic frontier cost model, 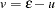 and
and
 |
The log-likelihood function for the production model with 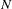 producers is written as
producers is written as
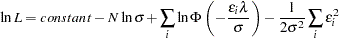 |
The Normal-Exponential Model
Under the normal-exponential model,  is iid
is iid  and
and 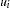 is iid exponential. Given the independence of error term components
is iid exponential. Given the independence of error term components 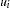 and
and  , the joint density of
, the joint density of  and
and  can be written as
can be written as
 |
The marginal density function of  for the production function is
for the production function is
 |
 |
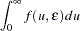 |
|||
 |
 |
 |
and the marginal density function for the cost function is equal to
 |
The log-likelihood function for the normal-exponential production model with 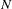 producers is
producers is
 |
The Normal-Truncated Normal Model
The normal-truncated normal model is a generalization of the normal-half normal model by allowing the mean of 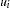 to differ from zero. Under the normal-truncated normal model, the error term component
to differ from zero. Under the normal-truncated normal model, the error term component  is iid
is iid  and
and 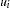 is iid
is iid 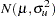 . The joint density of
. The joint density of  and
and 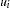 can be written as
can be written as
 |
The marginal density function of  for the production function is
for the production function is
 |
 |
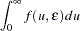 |
|||
 |
 |
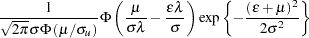 |
|||
 |
 |
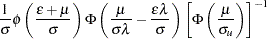 |
and the marginal density function for the cost function is
 |
 |
 |
The log-likelihood function for the normal-truncated normal production model with 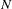 producers is
producers is
 |
 |
 |
|||
 |
 |
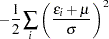 |
For more detail on normal-half normal, normal-exponential, and normal-truncated models, see Kumbhakar and Knox Lovell (2000) and Coelli, Prasada Rao, and Battese (1998).
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.