The PANEL procedure outputs the results of one specification test for fixed effects and two specification tests for random effects.

For fixed effects, let 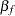be the dimensional vector of fixed-effects parameters. The specification test reported is the conventional F statistic for the hypothesis 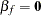. The F statistic with 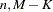degrees of freedom is computed as

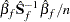where 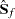is the estimated covariance matrix of the fixed-effects parameters.

Hausman’s (1978) specification test or m statistic can be used to test hypotheses in terms of bias or inconsistency of an estimator. This test was also proposed by Wu (1973) and further extended in Hausman and Taylor (1982). Hausman’s m statistic is as follows.

Consider two estimators, 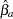and 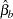, which under the null hypothesis are both consistent, but only 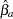is asymptotically efficient. Under the alternative hypothesis, only 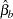is consistent. The m statistic is

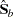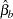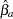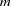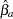where and are consistent estimates of the asymptotic covariance matrices of and . Then is distributed with degrees of freedom, where is the dimension of and .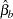

In the random-effects specification, the null hypothesis of no correlation between effects and regressors implies that the OLS estimates of the slope parameters are consistent and inefficient but the GLS estimates of the slope parameters are consistent and efficient. This facilitates a Hausman specification test. The reported statistic has degrees of freedom equal to the number of slope parameters.

Breusch and Pagan (1980) lay out a Lagrange multiplier test for random effects based on the simple OLS (pooled) estimator. If 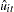is the th residual from the OLS regression, then the Breusch-Pagan (BP) test for one-way random effects is

The BP test generalizes to the case of a two-way random-effects model (Greene 2000, page 589). Specifically,

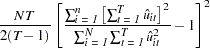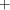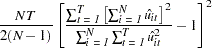is distributed as a 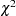statistic with two degrees of freedom. Since the BP2 test generalizes (nests the BP test) the test for random effects, the absence of random effects (nonrejection of the null of no random effects) in the BP2 is a fairly clear indication that there will probably not be any one-way effects either. In both cases (BP and BP2), the residuals are obtained from a pooled regression. There is very little extra cost in selecting both the BP and BP2 test. Notice that in the case of just groupwise heteroscedasticity, the BP2 test approaches BP. In the case of time based heteroscedasticity, the BP2 test reduces to a BP test of time effects. In the case of unbalanced panels, neither the BP nor BP2 statistics are valid.

Finally, you should be aware that the BP option generates different results depending on whether the estimation is FIXONE or FIXONET. Specifically, under the FIXONE estimation technique, the BP tests for cross-sectional random effects. Under the FIXONET estimation, the BP tests for time random effects.

While the Hausman statistic is automatically generated, you request Breusch-Pagan via the BP or BP2 option (see Baltagi 1995 for details).